Seeing the Matrix: A First-Principles Approach to Computer Architecture
Building a mental model of computer architecture from first principles
“Do not try to bend the spoon. That's impossible. Instead, only try to realize the truth... there is no spoon.” — The Matrix
The Matrix movie is profound in its metaphor of illusion and reality. There’s a scene where a child tells Neo: “Do not try to bend the spoon. That’s impossible. Instead, only try to realize the truth… There is no spoon.”
Modern computing is like that. We work in a reality constructed from abstractions: data types, functions, memory models, objects. But at the hardware level, none of it truly exists. It’s all just bits flowing through circuits made of silicon and metal, following instructions with no awareness of the abstractions we impose.
The diagram below illustrates the hierarchy of abstractions in computing. As software engineers, we usually work at the higher levels, writing code in languages like C, C++, or Rust. But these layers are built on top of deeper levels that are often hidden from view.
In this article, we will take the red pill and learn to see the reality as is. We will begin with the simplest building blocks: transistors and logic gates. From there, we will construct essential computational units like adders and registers, and see how these pieces fit together to form a working processor. By the end of this article, you will have a concrete model of how your high-level code is translated to machine code, and then executed at the level of logic gates.
Let’s begin!
This article is a prerequisite reading for our upcoming course on X86 assembly. If you have signed up for the course, do read it!
Download the PDF Version
This in-depth article spans over 5,000 words and includes several detailed diagrams to enhance your understanding.
If you'd prefer a neatly formatted, downloadable PDF version for easy reference or offline reading, it's available on Gumroad.
(Paid subscribers can get it for free. Check the email header for a discount code, or email me).
Building a Very Simple Processor
Real processor architectures such as X86 or RISC-V are for general-purpose computation and thus very complicated. We can better understand the design of the hardware by focusing on a much simpler use case, a simple calculator.
Even the calculator is capable of doing myriads of arithmetic computations, so to begin with, we will focus on just one computation: adding two integers. Essentially, we want a simple computer capable of expressing and computing the following computation:
int a = 10
int b = 20
int sum = a + bTo be able to do this, what capabilities do we need in the hardware?
We need a way to represent information: How do we represent data such as the integers 10 and 20 here, and also how do we tell the hardware that it has to add the two values?
Storing the input and output data: Where do these values of a and b live?
Doing the actual computation: How do we perform the addition in the hardware?
This line of inquiry leads us to the work done by Claude Shannon where we will find all our answers.
Encoding Information using Binary
You might be familiar with Claude Shannon’s work on information theory, which is the foundation underlying all modern communication systems and data compression techniques.
As part of this work, he came up with the idea of using electrical switches to encode information as binary data. Essentially, if we represent the state of the circuit when it is closed as 1 and when it is open as 0, then we can encode 1 bit of information in that circuit, and by combining multiple such circuits, we can encode more information.
By encoding information in binary, we can leverage the power of binary arithmetic and Boolean algebra to implement complex computational and logical calculations, giving way for general-purpose computation, which are modern computers.
Transistors as Digital Switches
But modern processors aren’t built using electrical switches, they are built using digital switches that can be turned on and off automatically. This is made possible through transistors.
Transistors are semiconductor devices that act as electronic switches. They conduct current only when the voltage applied to them is above or below a certain threshold, depending on their configuration. This ability to switch on or off based on voltage levels makes them ideal for implementing digital circuits. By precisely controlling the flow of current through circuits built from transistors, digital switches are created. These switches form the fundamental building blocks of all modern chips.
Transistors to Logic Gates
Transistors are the bottommost layer of the computing stack based on which everything else is built. They are combined in specific configurations to build reusable components called logic gates.
You can think of gates as mathematical functions (or, if you prefer code, then a function in code) that takes one or more inputs and produces an output. Because we are working with digital circuits, all the inputs and outputs here are 1s and 0s.
For instance, the NOT gate takes one parameter as input and produces one output. As its name suggests, it inverts its input. So NOT(1) = 0 and NOT(0) = 1.
Similarly, there is an AND gate that takes two inputs and produces one output (you can also make an AND gate that takes a larger number of inputs). Mathematically, it works like this:
AND(0, 0) = 0
AND(0, 1) = 0
AND(1, 0) = 0
AND(1, 1) = 1We also have an OR gate which works like this:
OR(0, 0) = 0
OR(0, 1) = 1
OR(1, 0) = 1
OR(1, 1) = 1Finally, there is a very useful gate called XOR:
XOR(0, 0) = 0
XOR(0, 1) = 1
XOR(1, 0) = 1
XOR(1, 1) = 0Boolean algebra establishes that by combining these basic operations, it is possible to compute any mathematical function, and this is how the computational circuits within the processor are designed. Let’s see how.
Building Computational Circuits from Logic Gates
So we started with the goal of implementing the functionality to add two integers in our simple hardware. And now we know that it can be accomplished using logic gates. The logic circuit which implements binary addition is called an adder. But, before looking at the circuit itself, let’s talk about binary addition.
Again, we can think of it like a mathematical or programming function. It receives two bits as input and produces two bits as output. One of the output bits represents the sum of the two input bits, and the 2nd output bit represents the overflow or carry of the result.
add(0, 0) = sum: 0, carry: 0
add(0, 1) = sum: 1, carry: 0
add(1, 0) = sum: 1, carry: 0
add(1, 1) = sum: 0, carry: 1
What you will see is that the mapping of the input bits to the sum value is identical to that of the XOR gate, while the mapping of the carry bit is identical to that of the AND gate. It means that an adder can be implemented by sending the input to an AND gate and a XOR gate, like the following figure:
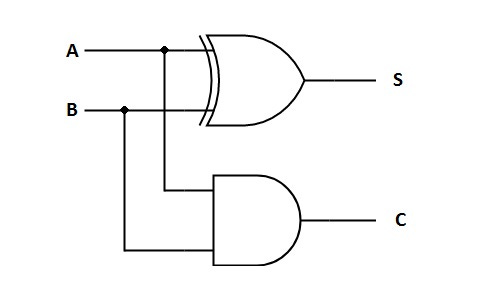
This design is called a half adder because it is not useful when adding multibit numbers. For addition of two multibit numbers, we need three inputs: two input bits from the numbers at a given position, and one carry bit from the addition of bits at the previous position. For this, a slightly modified circuit is used, called the full adder.
I will not show its construction because this article is not about digital design, but the following circuit shows what it looks like. By chaining these adders together, we can create circuits capable of adding multibit numbers.
The ALU
A real-world processor consists of multiple different kinds of computational circuits for operations such as addition, subtraction, multiplication, division, and also logical operations (AND, OR, NOT). These circuits are combined in the form of an arithmetic logical unit (ALU) and the various computational circuits within it are called functional units.
The inputs flow into the ALU which activates the right functional unit and produces the output. Schematically for our simple processor it looks the following diagram.
The Need for Storage: Introducing Registers
As you can see in the ALU diagram, it receives some input, performs the computation, and produces an output. So, the question arises: from where do these inputs come and where does the result go afterward? The answer is registers.
Apart from building computational circuits, transistors can be used to construct circuits that can hold state as well, i.e. memory. Using such circuits, we can construct memory units, and one such unit is the register.
Registers are fixed-sized memory units capable of storing a small number of bits, for example, modern processors have 32 or 64 bit wide registers. These are used to temporarily hold the data during computation. For instance, when performing an add operation, the input parameters are first stored in the registers, and then their values are fed into the ALU to perform the computation.
Typically, during program execution, data is moved into the registers from main memory (the RAM) and after the computation is done, the result is written back to the main memory. This frees up the register for other computations.
In our example of building a simple calculator, we need:
Two registers to hold the numbers we want to add (let’s say R1 and R2)
One register to hold the result of the addition. However, we could also use one of the two registers to store the output.
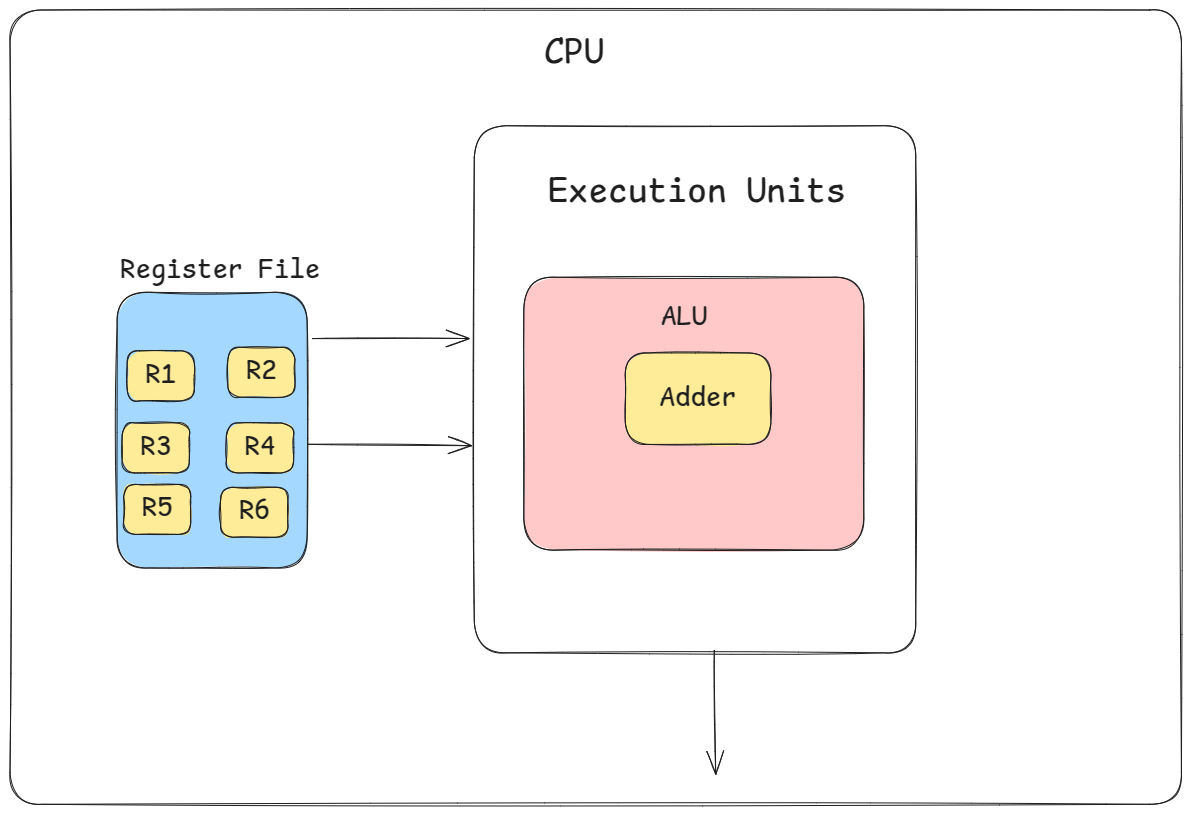
But real-world processors have many registers, e.g., the X86 architecture has 16 general-purpose registers. These registers are combined into a register file from which the data flows into the ALU. Let’s update the architecture diagram of our processor to see how it looks after the introduction of a register file consisting of 6 registers :
The diagram has started to show the typical organization of computer hardware at an abstract level. Typically, the ALU isn’t the only execution unit within the processor, so we have abstracted it inside an execution unit. The data flows from the register file into the execution unit to execute the instructions, and an output comes out of the execution units. As we go along, we will furnish more details in the diagram.
At this stage, our ALU is extremely limited; it can only perform an addition. Let’s extend it.
Adding Features and Control to Our Calculator
A processor capable of just addition is not very useful. We need more features, such as subtraction, multiplication, and division. All of these require computational circuits similar to the adder.
For example, subtraction can be implemented using the adder itself by simply negating the second operand value. But operations like multiplication need their own specialized circuits. We can implement these additional operations by adding separate circuits for each one, resulting in a more functional ALU with multiple functional units.
While we discussed the construction of the adder at the level of logic gates, we will not cover the remaining circuits at that level of detail. While that knowledge is valuable, as software engineers, it is not necessary to understand how everything works at the circuit level.
With multiple functional units in the ALU and multiple registers, we need a way to control which operation is performed and which registers are involved. This is done by a component of the processor, called the control unit.