Binary Arithmetic and Bitwise Operations for Systems Programming
Understand how computers represent numbers and perform operations at the bit level before diving into assembly
In our previous article, we explored how computers work from transistors up to program execution. We saw how digital circuits built from logic gates perform calculations using binary data, and how the ALU executes operations on this binary representation.
Now we’ll dive deeper the binary number system. When writing assembly code, you’ll directly manipulate bits in registers, perform calculations at the bit level, and for that you need to understand exactly how the processor interprets the patterns of 1s and 0s.
This article covers four key areas:
Number systems: How binary and hexadecimal work, and why we use them in low-level programming
Binary arithmetic: How computers add and subtract, and detect conditions like overflow
Two’s complement: How the hardware represents negative numbers
Bitwise operations: bit manipulation techniques used throughout systems programming
These concepts appear repeatedly in assembly programming, from register manipulation to optimized algorithms. By developing an intuition for binary operations, you’ll gain deeper insight into how processors work and how to write efficient assembly code.
Read it in PDF Form
This article is part of the material I’m developing for my X86 assembly course, that I am also putting together in a PDF form. If you are a paid subscriber you can claim it for free using the discount code in the email header (or ask me for the code).
Number Systems: Decimal, Binary, and Hexadecimal
The Decimal System: Our Familiar Base-10
The decimal system is so natural to us that we rarely think about why we use it. It has 10 distinct digits (0-9), and the position of each digit represents a power of 10:
For example, the following figure shows the representation of the decimal number 4,729
This system is called “base-10” or “radix-10” because it uses 10 as its base value for positional notation.
The Binary System: Base-2
Computers use the binary system (base-2) because digital circuits have two stable states. As we saw in our previous article, transistors function as switches that are either on or off, which naturally maps to 1 and 0. The logic gates built from these transistors process binary data, making binary the native language of all digital hardware.
In binary, each position represents a power of 2 rather than a power of 10:
For example, the following figure shows the broken down representation of the binary number 1011
Which equals 8 + 0 + 2 + 1 = 11 in decimal.
Converting from decimal to binary involves repeatedly dividing by 2 and tracking the remainders. Let’s convert 27 to binary:
27 ÷ 2 = 13 remainder 1 (least significant bit)
13 ÷ 2 = 6 remainder 1
6 ÷ 2 = 3 remainder 0
3 ÷ 2 = 1 remainder 1
1 ÷ 2 = 0 remainder 1 (most significant bit)
Reading the remainders from bottom to top: 11011, which is indeed 27 in binary.
Bit and Byte Terminology
When working with binary data, we need precise terminology to refer to specific portions of the data. The following terms are essential in assembly programming:
Most Significant Bit (MSB) and Least Significant Bit (LSB)
Binary numbers have two "ends" that are particularly important:
Least Significant Bit (LSB): This is the rightmost bit in a binary number. It represents the 2^0 (1) position and contributes the smallest value to the total. The LSB tells us whether the number is odd or even (1 = odd, 0 = even).
Most Significant Bit (MSB): This is the leftmost bit in a binary number. It represents the highest power of 2 in the value and contributes the largest amount to the total.

Most Significant Byte (MSB) and Least Significant Byte (LSB)
When working with multi-byte values (like 16-bit, 32-bit, or 64-bit numbers), we also need terminology for the bytes themselves:
Least Significant Byte (LSB): This is the byte containing the least significant bits of a multi-byte value.
Most Significant Byte (MSB): This is the byte containing the most significant bits.
For example, the 16-bit hexadecimal value 0x4A3F consists of two bytes:
- The MSB is 0x4A
- The LSB is 0x3F

Note about byte order: When multi-byte values are stored in memory, the order of the bytes becomes important. Different computer architectures may store the bytes in different orders (most significant byte first or least significant byte first). This concept, called "endianness," will become relevant when we discuss memory operations in later parts.
The Hexadecimal System: Base-16
Binary representation quickly becomes unwieldy when dealing with larger numbers. A 32-bit value would require 32 binary digits, which is difficult to read and prone to error. This is where the hexadecimal system (base-16) becomes valuable.
Hexadecimal uses 16 symbols: 0-9 and A-F (where A=10, B=11, …, F=15). Each hexadecimal digit represents exactly 4 binary digits (a “nibble”), making conversion between binary and hexadecimal straightforward.
This compact representation makes hexadecimal particularly useful for expressing binary values. For example, the binary number 1011010010011110 can be more compactly written as 0xB49E in hexadecimal. The “0x” prefix is a common notation indicating a hexadecimal number.
To convert this back to decimal:
B = 11 × 16³ = 11 × 4096 = 45056
4 = 4 × 16² = 4 × 256 = 1024
9 = 9 × 16¹ = 9 × 16 = 144
E = 14 × 16⁰ = 14 × 1 = 14
Adding these values: 45056 + 1024 + 144 + 14 = 46238
Why These Number Systems Matter in Assembly
When working with assembly language, you’ll constantly use all three number systems:
Binary is the processor’s native language. All the data in memory and registers is represented in binary and understanding this representation makes it easier to manipulate it.
Decimal is useful for human-friendly values and calculations.
Hexadecimal serves as the standard representation for memory addresses because it is easier to read than binary.
In assembly, you’ll typically express values in decimal or hexadecimal:
10 # Decimal 10
0Ah # Hexadecimal A (decimal 10)
0x0A # Alternative hexadecimal notation
Binary Arithmetic
Having explored how numbers are represented in binary, let’s now look at how computers perform calculations on these binary values.
Binary Addition
Binary addition follows similar rules to decimal addition, but with only two digits:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 with a carry of 1Let’s add the binary numbers 1011 (11 in decimal) and 101 (5 in decimal):
The result, 10000, is 16 in decimal, which is 11 + 5.
This calculation mirrors exactly what happens in the ALU’s adder circuit we examined previously. The carry bits generated during this process are physically propagated through the full adder circuits chained together to handle multi-bit addition.
The Processor’s Status Flags
To manage the results of operations, processors maintain a set of status flags that indicate various conditions. These flags are stored in a special register called the status register or flags register.
Four particularly important flags are:
Carry Flag (CF): Set when an unsigned arithmetic operation produces a carry or borrow
Zero Flag (ZF): Set when an operation produces a result of zero
Sign Flag (SF): Set when an operation produces a negative result (the most significant bit is 1)
Overflow Flag (OF): Set when a signed arithmetic operation produces a result outside the representable range
These flags are automatically updated after most arithmetic and logical operations. They’re crucial for implementing control flow in assembly code, as they allow the program to make decisions based on the results of calculations.
Understanding the Carry Flag
Because of the fixed-width registers in the processor, there is always a likely chance for the arithmetic operations to result in values that are too big to fit in the registers, i.e., the operations result in the generation of a carry.
To track these carries, the processor sets the carry bit in the flags register (in X86-64, the register name is rflags). The carry flag comes handy in several situations. Let’s discuss these.
Detecting Unsigned Overflow
The most straightforward use of the carry flag is to detect when an arithmetic result is too large to fit in the available bits - a condition called overflow.
For example, imagine adding two 8-bit unsigned numbers 242 and 18.
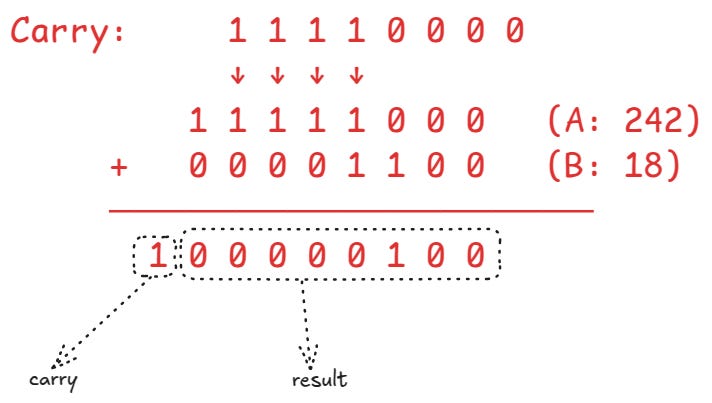
The result, 260, doesn’t fit in 8 bits (which can only represent values from 0 to 255). The “1” at the left falls outside our 8-bit range. The processor sets the carry flag to indicate this overflow condition.
Why is this important? In real programs, if you don’t detect overflow, your calculations will silently produce incorrect results:
The actual stored result would be just
00000100(4 in decimal)Your program would continue using this wrong value (4) instead of the correct result (260)
Consider an accounting program that adds large financial values, undetected overflow could cause funds to “disappear”!
Multi-Precision Arithmetic
“Multi-precision arithmetic” simply means working with numbers that are larger than what fits in a single register.
For example, let’s say we’re using an 8-bit processor but need to add two 16-bit numbers. We’d need to:
Add the lower 8 bits of both numbers
Add the upper 8 bits of both numbers
Account for any carry from the first addition
Here’s how it works, adding 1000 (0x03E8) + 2000 (0x07D0):

The result is 0x0BB8, which is 3000 in decimal. Without tracking the carry from the first addition, we would get 0x0AB8 (2744), which is wrong.
Assembly languages provide special instructions for these operations. For example, in x86, the adc (add with carry) instruction adds two values plus the carry flag, making multi-precision arithmetic possible.
The Foundation of Comparison Operations
The carry flag is also used for comparing unsigned values. When the processor compares two values, it actually subtracts them and sets flags based on the result, without storing the subtraction result.
For example, when comparing unsigned values A and B:
If A < B, the subtraction A - B requires a borrow, setting the carry flag
If A > B, no borrow is needed, clearing the carry flag
if A == B, the zero flag is set, indicating the values are equal
By checking the value of the carry flag we can figure out the result of the comparison, whether it was true or false, and execute appropriate code. When we learn about implementing conditional flow (if conditions) in assembly, we will see how this comes into action.







