Big O vs Hardware: Better Complexity ≠ Better Performance
Why Your O(log n) Algorithm Might Lose to O(n)
In algorithm design, we often rely on time complexity to compare solutions. It tells us how the work done by an algorithm grows with the size of its input. But real-world performance also depends on how well the code runs on hardware.
In a previous article, we explored the Iron Law of performance, which states that a program’s performance on the hardware depends on two factors:
Instruction count: fewer instructions usually mean faster execution.
Instructions per cycle (IPC): the more instructions a CPU can retire per cycle, the better.
By definition, algorithms with better time complexity tend to do less work. But they don’t always perform better if that work is harder for the CPU. A lower instruction count doesn’t help if each instruction is expensive or slows down IPC.
In this article, we’ll see a concrete example of this tradeoff. We’ll compare three algorithms for computing the greatest common divisor (GCD), study their time complexities, benchmark their real-world performance, and use the Iron Law to understand what’s really going on. As we will see, having a better time complexity is not a guarantee of better performance, a hardware friendly implementation also matters.
Euclid’s Subtraction-based Algorithm for Computing GCD
The first algorithm we will study is Euclid's subtraction-based algorithm for computing the GCD of two integers.
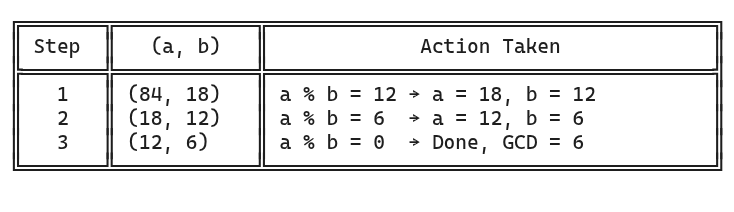
The GCD of two integers a and b is defined as the greatest integer that divides both a and b. For example, the GCD for 12 and 8 is 4. Euclid's subtraction-based algorithm for computing this is shown in the following code block.
gcd(long a, long b)
{
while (a != b) {
if (a > b) {
a -= b;
} else {
b -= a;
}
}
return a;
}The algorithm keeps removing the smaller number from the larger one until both of them become equal. Let’s trace an example with a = 84, b = 18.
As you can see in the above table, the algorithm converges in 7 steps.
Now, let’s think about the worst case time complexity of this algorithm. At each step the algorithm converges towards the GCD value by a step size that is equal to the difference between a and b. The smallest step possible is 1 when either a=1 or b=1. In that case, the algorithm will take as many steps as max(a, b), giving us the worst case time complexity as O(max(a, b))
In simpler terms, the algorithm grows linearly as the difference between a and b grows. For cases, when a and b are nearby, the algorithm converges quickly but when a and b are far apart, it will take a large number of steps.
This subtraction-based approach works, but there's a version that converges faster using division instead of repeated subtraction. Let’s take a look at that.
The Modulo-based Euclidean Algorithm for GCD
A more efficient variation of the Euclidean algorithm replaces repeated subtraction with division, reducing the number of steps required. The following snippet shows the code.
gcd(long a, long b)
{
while (b != 0) {
long t = b;
b = a % b;
a = t;
}
return a;
}We can trace the same input to see how this version behaves.
In this case, the algorithm converges in just three steps as compared to seven taken by the subtraction-based algorithm. It is easy to see that at each step the algorithm converges towards the solution by performing a division between a and b, which leads to the worst case time complexity of O(log(max(a, b))).
These time complexities give us a theoretical bound of the scale of these algorithms but the actual performance can be measured only by running on real hardware. Let’s run both algorithms on large inputs to see how their time complexity translates to actual performance.
Benchmark #1: Huge Inputs
As an example, let’s compare the performance of the two algorithms on the input a=1000000000 and b=9223372036854775503. Following figure shows the timing and other high-level performance metrics using the Linux perf tool.
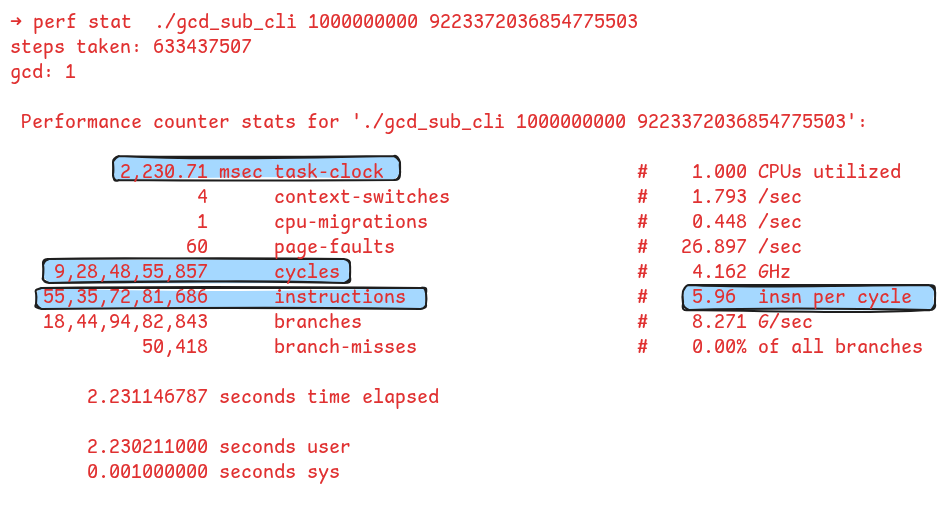
a=1000000000 and b=9223372036854775503The subtraction-based algorithm took 63,34,37,507 steps and ran in 2,230.71 milliseconds, consuming 9.28 billion CPU cycles. It executed 55.35 billion instructions at a rate of 5.96 instructions per cycle.
Now, let’s run the modulo-based algorithm and see how that performs.
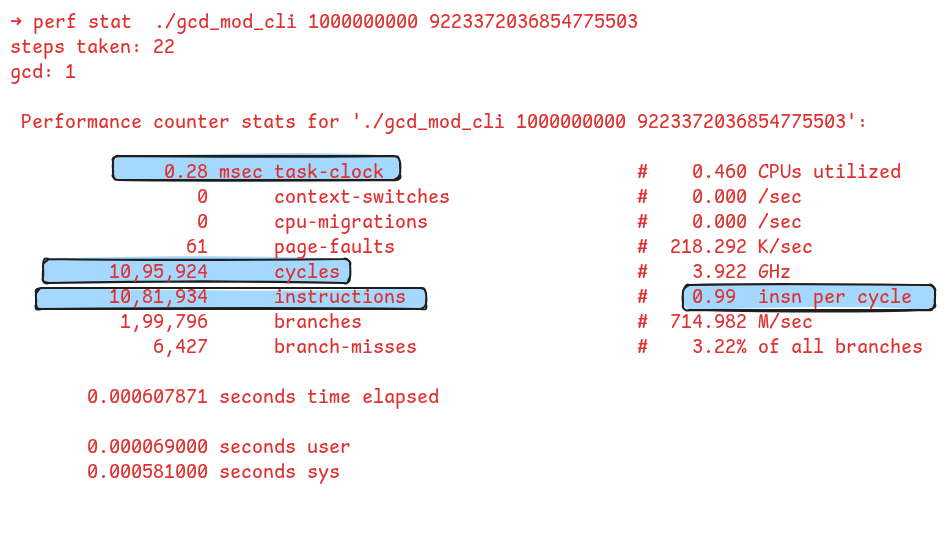
As expected, the modulo-based algorithm is dramatically faster, converging in just 22 steps. The CPU executes this in just 0.28 milliseconds, roughly 10,000x faster than the subtraction-based algorithm. It executed only about 1 million instructions and cycles.
This is algorithmic efficiency in action. However, it is not the ultimate truth. The performance of these algorithms also depends on the efficiency of the hardware-level operations. Let’s talk about that for a moment.
Cost of Integer Add vs Integer Division in Hardware
Time complexity tells us how the CPU workload scales with input size. Specifically, the work in the case of these two algorithms refers to subtraction and modulo operations. Inside the CPU, subtraction is performed by the execution unit that performs addition and modulo translates into integer division which is handled by a different execution unit.
So, the performance of these algorithms also depends on the efficiency of these fundamental operations. When talking about the efficiency of CPU instructions like these, we usually care about two aspects:
Latency: How many cycles does the CPU take to execute that instruction. The lower the latency, the better.
Throughput: How many of those instructions can the CPU execute each cycle. A processor may be able to execute more than one instruction of a certain type per cycle. Some instructions are pipelined. Even if one takes multiple cycles to finish, the CPU can begin executing another of the same type in the meantime. In addition to that, the processor may have multiple execution ports that can execute that operation in parallel.
On Intel Skylake processors, an add instruction has a latency of 1 cycle and a throughput of 4 operations per cycle because the hardware has four execution ports capable of performing integer addition. Often, the compiler takes advantage of this high throughput by unrolling loops when it notices the loop involves addition operations.
On the other hand, integer division is very expensive. On Intel Skylake, it has a latency of 42-95 cycles. Unlike integer addition, there is only one execution port capable of performing integer division, as a result you can execute only one integer division operation every 24-90 cycles (as per Agner Fog’s optimization manual).
This contrast in the performance of these operations brings the Iron Law into the picture. The subtraction-based algorithm will always execute a higher number of instructions, but it will also have a better IPC. On the other hand, the modulo-based algorithm will execute less number of instructions, but it will have a very poor IPC. Performance depends on the tradeoff between instruction count and IPC. Let’s do another benchmark to see this play out.
Benchmark #2: Small Inputs
In this next benchmark, we use inputs that are close in value to observe how IPC can dominate when instruction counts are similar. The following table summarizes the performance of these two algorithms for the input where a=130000, b=13.
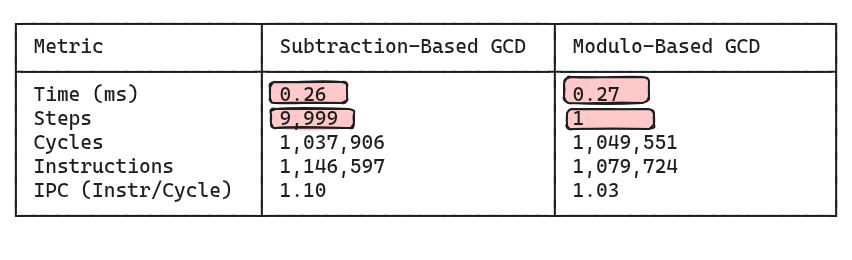
The subtraction-based algorithm executes 9,999 steps as compared to the modulo-based algorithm that converges in a single step. Despite taking 10,000 steps, the subtraction-based algorithm finishes 1 millisecond faster.
If we apply the Iron Law lens, we can see that the subtraction-based algorithm executed a slightly higher number of instructions, but it had a slightly better IPC as well which tipped the performance in its favor.
This isn’t to say algorithmic complexity doesn’t matter, at large scales, it absolutely does. But, a lot of the workload may never hit those scales and the implementation needs to take that into account. For example, many sorting routines use quicksort for large arrays, but switch to insertion sort for smaller sizes (e.g. fewer than 5 elements) because it’s simpler and faster in that regime. Similar strategy can be employed here. For values with smaller gap between them, subtraction-based algorithm can be preferred, while for values with larger difference, modulo-based algorithm can be used.
An alternative to switching between algorithms is to use an implementation that’s inherently hardware-friendly. In 1967, Stein designed such an algorithm that takes advantage of binary representation of integers and leverages bit shift operations that are very fast at the hardware-level. Let’s first understand how it works before comparing performance.
Stein’s Binary Algorithm for GCD
Stein designed this algorithm based on certain observations about GCD computation. These are as follows:
gcd(a, b) = gcd(b, a)gcd(0, b) = b, andgcd(a, 0) = agcd(2a, 2b) = 2 * gcd(a, b), i.e., if a and b are even then we can compute the GCD of their halves and then multiply the result by 2.gcd(a, 2b) = gcd(a, b), i.e., if b is odd then 2 is not a common divisor.gcd(a, b) = gcd(a, b - a)when a and b are odd anda < b.
These observations lead to a recursive algorithm that reduces the inputs until b == 0. However, unlike the modulo-based algorithm, this algorithm can be highly optimized for real hardware. For example, most implementations use the following optimization tricks.
Instead of recursion, iteration is preferred.
Every step of the loop has to reduce a and b to odd values. This requires repeated division by 2. It turns out division by 2 can be done by the right bit shift operation which is much faster to perform than division.
The algorithm needs to check if the numbers are odd or not. Dividing by 2 and checking the remainder is not efficient because division is slow and introduces branches. A more efficient trick is to always ensure that the least significant bit (LSB) of these numbers is 1. This can be done by counting the number of trailing zero bits in the number, and right shifting by that many bits. Most processors have a dedicated instruction to count the number of trailing zero bits, so this is extremely cheap to do.
The following code block shows the C implementation of this algorithm (it uses the GCC builtin __builtin_ctzl to count the number of trailing zero bits).
gcd(long a, long b)
{
// base conditions
if (a == 0)
return b;
if (b == 0)
return a;
// gcd(2^i * a, 2^j * b) = 2^k * gcd(a, b)
// where k = min(i, j)
int k = __builtin_ctzl(a | b);
// make a odd
a >>= __builtin_ctzl(a);
while (b != 0) {
// make b odd
b >>= __builtin_ctzl(b);
// ensure b > a
if (a > b) {
long temp = a;
a = b;
b = temp;
}
// gcd(a, b) = gcd(a, (b-a)/2))
// the division by 2 happens in the next iteration
b = b - a;
}
// multiply 2^k back into the final gcd value
return a << k;
}
At each step of the iteration, the algorithm converges by dividing b by 2, so the worst case time complexity is O(log_2(max(a, b)), which is the similar as the modulo-based algorithm. But this algorithm has the advantage that it uses efficient hardware instructions. This means that the algorithm executes fewer instructions while maintaining a higher IPC, which is a win over the modulo algorithm.
With the theory and hardware considerations in place, let’s now compare all three algorithms side by side.
Benchmark #3: Comparing All Three Algorithms
First, let’s revisit the large-input benchmark: a=1,000,000,000 and b=9,223,372,036,854,775,503. The following table summarizes the key findings.
We see that the binary algorithm performs just as well as the modulo-based algorithm even though it takes a few extra steps to converge.
We can also analyse this using the Iron Law.
The subtraction algorithm executes 92 billion instructions, which is vastly higher than the ~1 million executed by the other two.
The IPC of the subtraction algorithm is very high but the high instruction count dominates because of which it takes significant amount of time to finish.
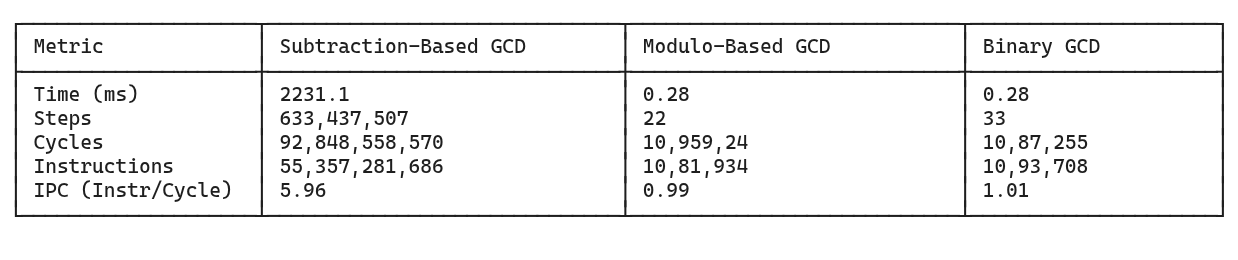
a=1,000,000,000 and b=9,223,372,036,854,775,503Next, let’s compare the performance for the 2nd input where a=130000, and b=13. The following table shows the numbers. In this case, we see that the binary algorithm matches the performance of the subtraction-based algorithm. This happens because not only it executes fewer instructions but uses efficient instructions, leading to a higher IPC. It strikes the ideal balance from the Iron Law’s perspective.
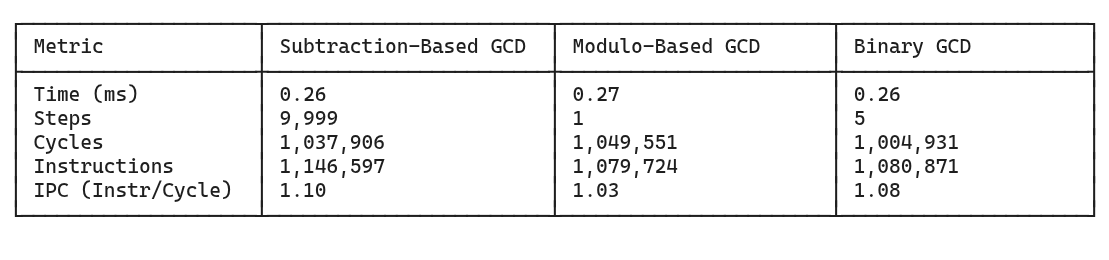
But comparing the performance on just two inputs is not enough. The following table shows the performance of these algorithms on a benchmark where they compute the GCD for all unique combination of values in the range [1, 100000).

Let’s analyse this for a moment:
The binary algorithm is the fastest, while the modulo-based algorithm is the slowest despite having the same time complexity as the binary algorithm. This highlights that a superior complexity is not the only thing that gets you performance, the hardware specific implementation is also crucial.
The modulo-based algorithm executed 13 billion instructions (the lowest) while the subtraction-based algorithm executed 97 billion instructions (the highest). Yet, the subtraction-based algorithm finished 1.5 seconds earlier. It highlights how efficient integer add operation is in processors as compared to division.
The subtraction-based algorithm had an IPC of 1.16 (the highest), while the modulo-based algorithm had the lowest IPC of 0.15.
The binary algorithm doesn’t win in instruction count or IPC. But it outperforms in the overall execution time because from the Iron Law’s point of view, it strikes the right balance between the two factors. In fact, if you benchmark these algorithms on a wide range of values, the binary algorithm always gives a consistent performance, while the performance of the other two algorithms can vary depending on the inputs.
Conclusion
Algorithmic time complexity is important, but real-world performance also depends on how well an algorithm maps to the underlying hardware. Doing less work doesn’t help if that work is inefficient or poorly suited to the CPU. The fastest implementations are those that align with the strengths of the hardware, such as low-latency instructions, high IPC, and predictable execution.
Code
All the code used in the analysis behind this article can be found in the GitHub repo linked below.