LZ77 Is All You Need? Why Gzip + KNN Works for Text Classification

Decoding the Success of Gzip + KNN: The Central Role of LZ77

“Any fool can know. The point is to understand” — Albert Einstein

In the previous article, we went over the Gzip + KNN paper. The paper demonstrated that using a combination of Gzip compression and k-nearest neighbors (KNN) for text classification achieves near state-of-the-art performance on many benchmarks. Even though the paper had a significant flaw in its evaluation method, it still yielded a level of accuracy that cannot be ignored. This raises an open question: why is compression so effective in text classification? In this article

Alejandro Piad Morffis

and I attempt to answer this question, examining various compression algorithms to uncover the core principle that makes this technique effective.

Synopsis: On closer examination of the compression methods evaluated by the paper, LZ77 is found at their core. This is likely the primary reason for the effectiveness of these algorithms. Read on If you're interested in understanding why and how.

To learn more about the gzip + KNN paper and its findings, I suggest reading my previous article.

Decoding the ACL Paper: Gzip and KNN Rival BERT in Text Classification

---

---

Understanding Gzip + KNN Based Text Classification: A Recap

To contextualize this article, let's briefly recap how the paper employed gzip and k-nearest neighbors for text classification. To categorize a particular sample t, we compress t and calculate its distance from every other compressed sample in the training data. We then assign the class of the nearest neighbor as the output of the classification algorithm.

The paper made use of the Normalized Compression Distance (NCD) to measure distances between two compressed pieces of text:

\(NCD(x, y) = \frac{C(xy) - min\{C(x), C(y)\}}{max\{C(x), C(y)\}} \)

Crucial elements of this equation include:

• C(x), the length, in bytes, of x after compression.

• C(xy), the length, in bytes, of the result when x and y are concatenated and then compressed.

The equation's numerator represents the shared information between `x` and `y`, while the denominator scales the distance within the [0,1] range.

The underlying concept of NCD is that two documents from the same class likely share a lot of common words and patterns. Consequently, their concatenation will result in better compression, as opposed to two documents from different classes. This theory is our primary clue. It suggests that the method capitalizes on common patterns between x and y, leading to a larger value for C(xy). It might appear that this is just the definition of compression, but we will see that not all compression algorithms are capable of this.

Introduction to Lossless Compression Algorithms

The paper evaluated four compression techniques for text classification: gzip, LZMA, zstandard (zstd) and bzip2. To fully understand these methodologies, we need to dissect them and analyze what is happening at a deeper level. All these algorithms are constructed by combining more basic compression techniques such as LZ77 and Huffman coding. Therefore, we will begin by understanding these building blocks before returning to Gzip, LZMA, zstd, and bzip2.

If you are familiar with these compression techniques, feel free to skip this section.

LZ77

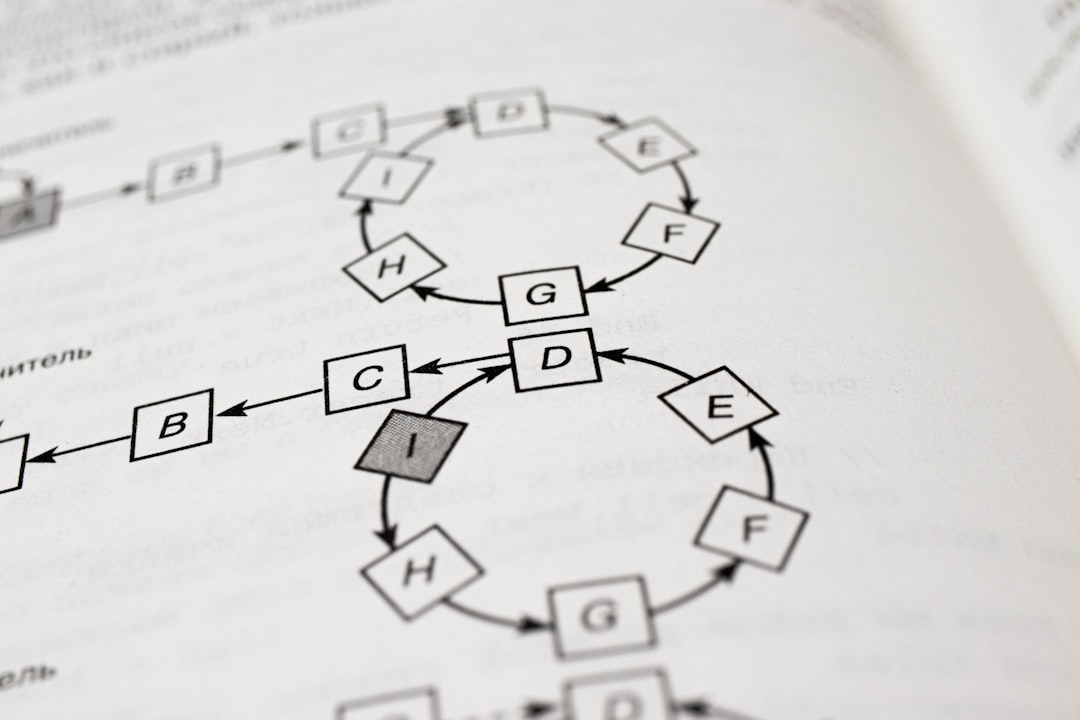
LZ77 is a dictionary-based compression algorithm developed by Lempel and Ziv in 1977. The fundamental idea in all dictionary-based compression algorithms is to replace repeating patterns in the text with references to their entries in a dictionary. LZ77 employs a sliding window-based search buffer as it scans the text. Any duplicate string patterns in the text are replaced by a reference to their latest instance in the sliding window. The reference is typically a pair of numbers: <offset, length>. The offset indicates the number of bytes to backtrack from the current position to reach the start of the match, and the length is the length of the match.

The following image shows how this might work when encoding the string “abracadabra”. When we reach the last part of the string “abra”, it has previously occurred at the beginning of the string, therefore we replace this 2nd occurrence of “abra” with a pointer having offset as 7 and length as 4.

Example of dictionary match in LZ77 Compression

In general, if repeating substrings are plentiful in the text, LZ77 achieves a high level of compression.

Statistical Coding Techniques

Statistical coding techniques form a category of compression algorithms rooted in the core concept of assigning shorter codes to symbols appearing frequently in the data and lengthier codes to symbols that occur less often. These algorithms operate by first formulating a probability distribution of the symbols in the data and then assigning codes to symbols based on their likelihood of appearing in the text.

Huffman coding, arithmetic coding, and asymmetric numeral systems (ANS) are the most well-known and widely-used examples of statistical coding techniques. Almost all compression methods (Gzip, LZMA, zstd, and bzip2) use one of these statistical coding techniques. While explaining each of these techniques in depth would require several dedicated articles, they all operate on the fundamental idea of assigning shorter codes to more frequent symbols, as previously discussed.

Run Length Encoding (RLE)

Run-Length Encoding (RLE) is among the simplest methods of compression. It replaces continuously repeating occurrences of symbols with a frequency count of their occurrence followed by the symbol itself. For instance, the string “aabcc” can be encoded as “2ab2c.”

Burrows-Wheeler Transform (BWT)

The Burrows-Wheeler transform (BWT) is not a compression technique itself but a preprocessing step which essentially rearranges the characters in the text to place similarly occurring characters together. The primary advantage of BWT is that it tends to group identical or similar characters in a way that enhances their compressibility by subsequent compression algorithms like Move-to-Front (MTF) or Run-Length Encoding (RLE).

The following example is taken from the Wikipedia page of BWT. It shows how the output maximizes the occurrences of IX, SS, PP and II. It is easy to see how this improves compressibility of the text by techniques such as RLE.

Input	SIX.MIXED.PIXIES.SIFT.SIXTY.PIXIE.DUST.BOXES
Output	TEXYDST.E.IXIXIXXSSMPPS.B..E.S.EUSFXDIIOIIIT

Breaking Down Compression Techniques: gzip, LZMA, zstd and bzip2

Now that we have covered the basic building blocks of compression algorithms, let’s look down inside the compression techniques the paper evaluated: gzip, LZMA, zstd and bzip2.

Gzip Compression

Gzip employs a compression algorithm called DEFLATE which operates in two stages:

• LZ77 Coding: In the first stage the text is compressed using LZ77.

• Huffman Coding: In the next stage, the output of LZ77 is further compressed using Huffman coding.

LZMA Compression

The LZMA (Lempel–Ziv–Markov chain algorithm) algorithm also operates broadly in two stages.

• LZ77 Coding: In the first stage it employs a variant of LZ77 based dictionary compression.

• Range Encoding: The output of LZ77 from the previous stage is further encoded using range encoder, which is another statistical coding technique similar to the ones we discussed previously.

ZStandard (zstd)

Zstandard (zstd) is a fairly new compression algorithm created by Yann Collet at Facebook. Zstd also operates in two main stages.

• LZ77 Coding: Zstd starts with LZ77 compression of the text

• Huffman Coding and Finite-state Entropy Coding: The output of LZ77 is further encoded using a combination of Huffman coding and finite-state entropy based coding. Finite-state entropy is another statistical coding technique based on asymmetric numeral systems (ANS).

Bzip2

Bzip2 is probably the most different of all of these algorithms. It employs multiple coding techniques and works in several stages.

• Burrows-Wheeler Transform (BWT): The input data is first subjected to the Burrows-Wheeler Transform, which rearranges the characters in a way that groups similar characters together, enhancing their compressibility.

• Move-to-Front (MTF): After the BWT, the MTF technique is applied. It transforms the BWT output by encoding the data into a sequence of integers.

  • MTF maintains a list of symbols (e.g., characters or bytes) in a specific order and updates the order dynamically as each symbol is processed.

  • When a symbol is encountered, it is encoded as the index of its position in the list, and then it is moved to the front of the list.

• Run-Length Encoding (RLE): Following MTF, the data is further compressed using Run-Length Encoding (RLE). RLE replaces consecutive repeated symbols with a single symbol and a count of its occurrences, reducing redundancy in the data.

• Huffman Coding: Finally bzip2 compresses the output of RLE by applying Huffman coding on it.

This is a very high-level description of the workings of these techniques. While several details are not covered here, the idea was to simply highlight these techniques' key components in order to investigate those components' role in text classification.

Identifying the Common Thread

According to the paper, gzip, LZMA, and zstd achieved extremely high accuracy on various benchmarks. However, bzip2 performed disappointingly. Upon viewing these compression techniques, we find a commonality: all employ some form of LZ77 coding followed by a form of statistical coding (usually Huffman coding). Bzip2 is the only one diverging from this method.

This is a strong hint that LZ77 may be the main reason behind the success of these algorithms in text classification. This hypothesis is rational since LZ77 compresses text by replacing repeated strings and two pieces of text from the same class will naturally contain many common words, enabling LZ77 to compress efficiently. Statistical coding techniques such as Huffman are applied to LZ77’s output, at which point the original text has already been substantially transformed. Furthermore, these statistical coding techniques operate at the symbol or character level, suggesting that they cannot take advantage of the fact that they are compressing text containing many frequent words and phrases

Verifying The LZ77 Theory Experimentally

Let's validate this LZ77 hypothesis through experimentation. Using a small dataset consisting of four classes — each with only two samples — allows us to investigate and understand what happens during compression; this becomes difficult with larger datasets.

The Dataset

We are going to use a tiny dataset consisting of 4 classes: Sports, Astronomy, Cooking, and Gardening, with each class having 2 sample. The dataset is shown below:

classes = {
    "Sports": [
    """
    Football is a popular sport enjoyed by millions worldwide
    The players engage in fierce competition with the aim of
    scoring the most goals. The tactics and strategies employed
    by different teams often play a critical role in their success.
    The exhilarating experience of watching a football match in a
    stadium full of passionate fans is hard to match.
    """,
    """
    Cricket is a sport that requires a blend of physical fitness
    and strategic planning. It is loved by millions around the
    globe, especially in countries like England, Australia and
    India. The thrilling run chases, astounding catches, and
    nail-biting finishes are what make cricket a spectacular sport.
    """
    ],
    "Astronomy": [
    """
    The vastness of the universe is explored through astronomy.
    The study encompasses understanding celestial bodies such as
    the sun, stars, planets, and galaxies, and extraterrestrial
    phenomena. The quest for knowledge about the universe has
    led to iconic discoveries and advancements in technology.
    """,
    """
    Astrophysics, a branch of astronomy, seeks to understand the
    workings of stars, galaxies, and the cosmos as a whole.
    There are countless mysteries yet to be unraveled about the
    universe, from dark energy to the possibility of life
    elsewhere in the cosmos.
    """
    ],
    "Cooking": [
    """
    Cooking is an art that brings a fusion of flavors, textures,
    and aroma to the table. Several cooking methods, such as
    grilling, roasting, baking, boiling, and frying are used to
    create a culinary masterpiece. The mastery of cooking
    involves a fine understanding of ingredients and their
    intrinsic properties.
    """,
    """
    Gastronomy focuses on the discipline of cooking, focusing
    on the artistic, technical, and cultural aspects of food.
    Mastery in this field requires an appreciation for quality
    ingredients, technique, and cultural tradition.
    Experimentation adds to the artistry of gastronomy,
    resulting in unique, delectable dishes.
    """
    ],
    "Gardening": [
    """
    In her beautiful garden, Mary cared for various flowering
    plants and shrubs diligently. She knew the importance of
    regular watering, appropriate sunlight, and quality
    fertilizers. She nurtured roses, tulips, and sunflowers
    with utmost love and care.
    """,
    """
    Sarah was a passionate gardener, tending to an array of
    blooms and bushes with attentiveness. She acknowledged
    the significance of consistent irrigation, needed sunlight
    exposure, and effective fertilizers. She fostered roses,
    tulips, and sunflowers with abundant affection and care.
    """
    ]
}

Methodology

We are going to evaluate four compression algorithms on this dataset for text classification: Gzip, Huffman coding, LZ77 (we will use LZ4 since there are no readily available LZ77 Python implementations), and Bzip2 (not the full version, merely the BWT followed by MFT).

We will take each class sample and compute its distance (using NCD) from every other sample in the dataset (excluding distance from itself). We will report the nearest matching class and its distance.

Results

Nearest neighbour results for each of the compression methods on each sample and the value of the NCD function.

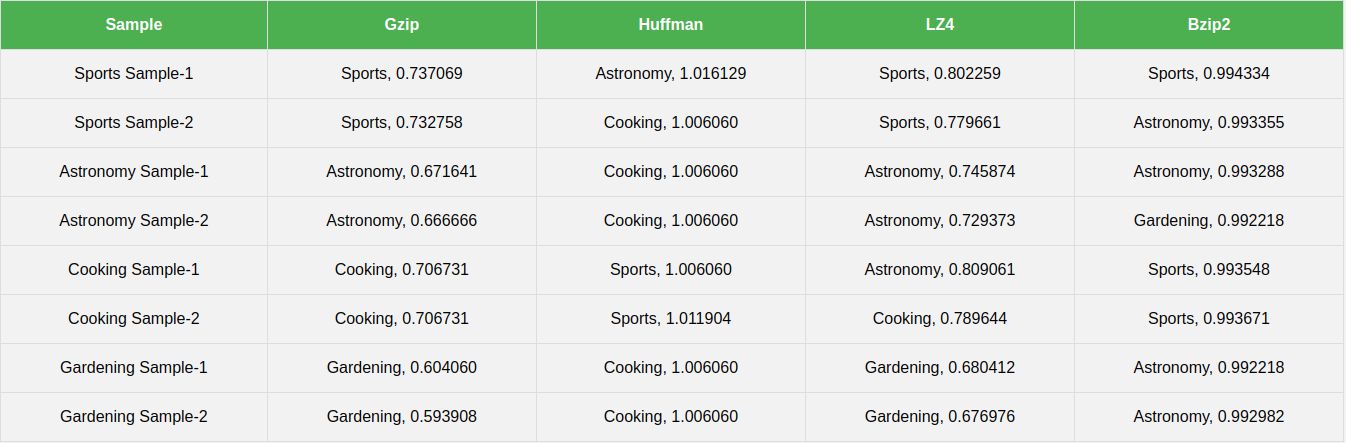
The above table shows the result of our little experiment. Here’s a summary of the results.

• Gzip: Gzip achieves a perfect score, matching each sample of the class with the other sample from the same class.

• Huffman Coding: Huffman coding performs the worst, it is not able to match any class correctly. The NCD distance value greater than 1 suggests that it was not able to compress the concatenation of the two samples, leading to a bigger numerator in NCD computation.

• LZ77/LZ4: LZ4 correctly classifies 7 out of the 8 samples. Incorrectly classifying one Cooking class sample as Astronomy is explainable as these two share more common words than the two Cooking samples. In a larger dataset with many more samples per class, this is less likely to happen as the chances of finding a neighbor within the same class increase with the number of samples in the class.

• Bzip2: In this experiment, Bzip2 isn't used in its entirety; only the BWT followed by MFT, which are the first two steps of bzip2, are applied. The aim was to check the effect of BWT on classification and it is visible that it does not contribute much when it comes to NCD. Perhaps this is why bzip2 underperforms as reported in the paper.

This small-scale experiment serves to demonstrate that LZ77 does indeed significantly contribute to the high accuracy of various compressors on text classification as showcased in the paper. Even though the paper mentions that different compressors are interchangeable, they may not be to a certain degree. For instance, bzip2's performance fell short, and Huffman coding failed spectacularly.

Related Work

• Matthias Minder has performed a full ablation study and measured performance of LZ77 on some of the datasets used in the paper. He also finds that LZ77 achieves high accuracy and works just as well as gzip.

• Sebastian Raschka, PhD
  evaluated the performance of gzip and KNN on the IMDB movie review dataset and found that it achieves close to 71% accuracy on it. He also writes about his evaluation and some of the performance improvements he made to speed up the process. Read about it here

  Large Language Models and Nearest Neighbors

• Cyril de Catheu implemented an alternate version of this technique using zstd. As running KNN on the entire training data to classify each single sample was exceedingly time-consuming, he utilized zstd dictionaries. The zstd library has the option to construct a pretrained dictionary from a sample dataset, which can then be used by the compressor to compress any text. He created dictionaries for each class in the training data and developed one compressor per class using those dictionaries. To classify a piece of text, he compressed it using each class-specific compressor and chose the class of the compressor that achieved maximum compression. Read more about it here.

Resources

All the code and data used for the above experiments is available on GitHub.

Wrapping Up

In conclusion, our exploration shed light on the mechanics behind the surprising effectiveness of the Gzip + KNN approach in text classification. Diving deep into the nitty-gritties of compression algorithms, it appears that the LZ77 and similar algorithms are central to its success due to their aptitude to leverage the repetitive nature of substrings, words, and phrases in text.

In fact, bag-of-words models come to mind when talking about reptitive words across two pieces of text. Interestingly, despite the original research paper neglecting to compare the Gzip + KNN method against a bag-of-words baseline, additional analysis by Juri Opitz indicated that bag-of-words models can attain comparable or even superior results.

However, the core takeaway from this exercise goes beyond the realm of text classification. It underlines the importance of considering more straightforward, accessible solutions before deploying complex, resource-intensive methods. This principle applies not just with regards to compression algorithms and text classification, but as a broader approach to problem-solving in the field of data science. Assessing simpler strategies first could lead to efficient solutions, emphasizing that sometimes, less really can be more.

---