How Language Models Beat PNG and FLAC Compression & What It Means

A detailed analysis of the DeepMind/Meta study: how large language models achieve unprecedented compression rates on text, image, and audio data - and the implications of these results

Recently, there has been a lot of interest in the use of compression in machine learning (e.g., using gzip + knn for text classification). Adding to that, DeepMind and Meta have released a new paper titled “Language Modeling Is Compression”. The paper builds on the idea that prediction is equivalent to compression and shows that when large language models are used as compressors, they achieve state-of-the-art compression rates on datasets of different modalities including text, image, audio. They also shed more light on other aspects of language models from the lens of compression, such as scaling laws, context window sizes, and tokenization.

Even though the experiments and results shown by this paper are intriguing, the paper is not an easy read—it builds upon some recent results, and if you are not on top of that work, you might find yourself lost. Also, the paper is not very clear on the main insights from its results, leaving you wondering what to take away from it. In this article, my objective is to explain the main ideas of the paper in simpler terms.

Photo by Mika Baumeister on Unsplash

---

Background on Compression Using Language Modeling

The paper is all about compression using large language models; therefore, let's cover some background on these topics before we talk about the results from the paper itself.

Statistical Compression Algorithms

The paper combines language models with statistical compression algorithms to compress the data. A statistical compression algorithm compresses data by using the probability distribution of symbols in the data. The basic idea is to assign shorter binary codes to symbols which have a high probability of occurrence while assigning longer codes to symbols with lower probabilities. This probability distribution can be built by the compression algorithm itself, or it can be provided externally. In the case of compressing data using language models, the output of the language model provides the probability distribution.

There are various statistical compression algorithms such as Huffman coding, arithmetic coding, and asymmetric numeral systems. The paper specifically uses arithmetic coding in its experiments, but it is replaceable with any other algorithm. The exact mechanics of arithmetic coding are not interesting here, so we don't need to concern ourselves with understanding the details of it.

Let's take an example. Consider our data consists of three symbols A, B, and C with probabilities 0.8, 0.15, and 0.05, respectively. Since A and B have the highest probabilities, we could assign them codes '0' and '1', while assigning a longer code '01' to C. Thus, when we encode any string using these shorter code, we will have a compressed representation as compared to the raw data.

Using Language Models for Compression

A language model takes a sequence of tokens as input in its context and outputs a probability distribution for the next token. When generating text, we select the token with the maximum probability from this output, add it to the context, and predict the next token.

There are more nuanced strategies than just picking the max probability token, but that’s not the topic of discussion here. You can read this guide to learn other techniques for selecting the next token.

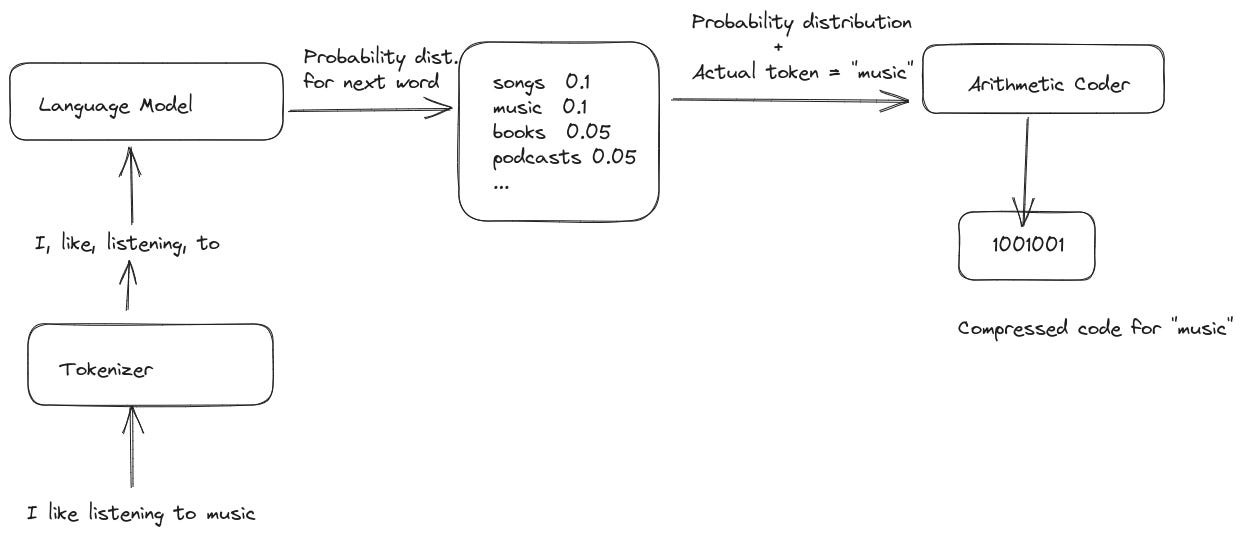
However, if we want to use the model to compress a piece of text, we will use it differently. In this situation, we would have the text that we want to compress available to us in its entirety. At any point in time, the model would have a sequence of tokens from the raw text in its context, and it will produce a probability distribution for the next token. At this point, we will also know the correct value of the next token from the raw text. We can feed this output probability distribution along with the actual value of the next token to an arithmetic coder to produce a compressed code. By repeating this process for each token in the raw text, we can compress it effectively. Let's understand with the help of an example.

Let's imagine we want to compress the text "I like listening to music", and the current context available to the model is "I like listening to". Based on this, the model outputs a probability distribution for the next word as follows:

P(music) = 0.5
P(songs) = 0.4
P(podcasts) = 0.3
P(books) = 0.1
...
P(cats) = 0.000001

Given the actual value of the next word, i.e., "music", and this probability distribution, an arithmetic coder (or any other statistical encoder) will be able to produce a compressed code for it.

The following illustration shows how this works when doing compression. It is heavily inspired by the example shown in the LLMZip paper.

Combining a language model and arithmetic coder to compress text

What Does this Mean?

Intuitively, the better a model is at predicting the right words with high probability, the more compressed codes the arithmetic coder will be able to produce, thus achieving significant compression. On the other hand, if the model is not good at prediction, it will output the expected words with low probability, and therefore, the arithmetic coder will not be able to produce efficient codes.

In the paper, the authors also use the LLM to compress images (and audio data). They do this by passing contiguous patches of images encoded in bytes. They find that they are able to achieve state-of-the-art compression with this data as well. This means that the model is able to take advantage of its in-context learning abilities to generalize to images and is able to predict the next byte(s) quite accurately, thus achieving high levels of compression. We will discuss these results later in the article.

---

Datasets and Models Evaluated in the Paper

The paper evaluated the compression performance of language models on datasets of different modalities: text, image, and audio. In order to be able to compare the compression performance on all of these, they restricted the dataset size to 1 GB for each of them. Following are the datasets they used:

• enwik9: The enwik9 dataset consists of the first 1 billion bytes of the Wikipedia English XML dump on March 3rd, 2006. It is an extension of the enwik8 dataset which consists of just the first 100 million bytes.

• ImageNet: The ImageNet dataset consists of 14,197,122 annotated images. The authors extract contiguous patches of size 32 x 64 from all images, flatten them, convert them to grayscale to obtain samples of size 2048 bytes. They concatenate 488,821 such patches in the original dataset order to obtain a dataset of size 1 GB.

• LibriSpeech: LibriSpeech consists of 1000 hours of English language speech at 16 kHz frequency. To create a dataset of 1 GB size, the authors chunk the samples into batches of size 2048 bytes and gather 488,821 such chunks.

Model Details

In the paper, the authors evaluate a vanilla decoder-only transformer model (pretrained on enwik8) and pretrained Chinchilla-like foundation models. They combine these models with arithmetic coding to perform compression.

Metrics: Raw Compression Rate and Adjusted Compression Rate

The paper compared the performance of the models by looking at the compression rate metric. They defined two flavors of this metric: raw compression rate, and adjusted compression rate.

The raw compression rate is computed as compressed size / raw size, and the lower the value, the better an algorithm is doing at compressing the data.

In the case of the adjusted compression rate, the model's size is also added to the compressed size, i.e., it becomes (compressed size + number of model parameters) / raw size. This metric allows us to see the impact of model parameters on the compression performance. A very large model might be able to compress the data better compared to a smaller model, but when its size is taken into account, the smaller model might be doing better. This metric allows us to see that.

With all this background covered, let's move on to looking at the results from the paper.

Key Insight 1: Achieving State-of-the-art Compression Rates on Multi-modal data

The first result shown by the paper is state-of-the-art compression rates achieved by language models on text, image, and audio data. The authors combined the language models with an arithmetic coder to compress the datasets. They evaluated vanilla Transformer models, Chinchilla models, along with compressors such as gzip, LZMA2, PNG and FLAC. The following table from the paper the results of their experiments.

Table-1 from the paper showing compression rates of different models and algorithms on enwik9, ImageNet and LibriSpeech datasets

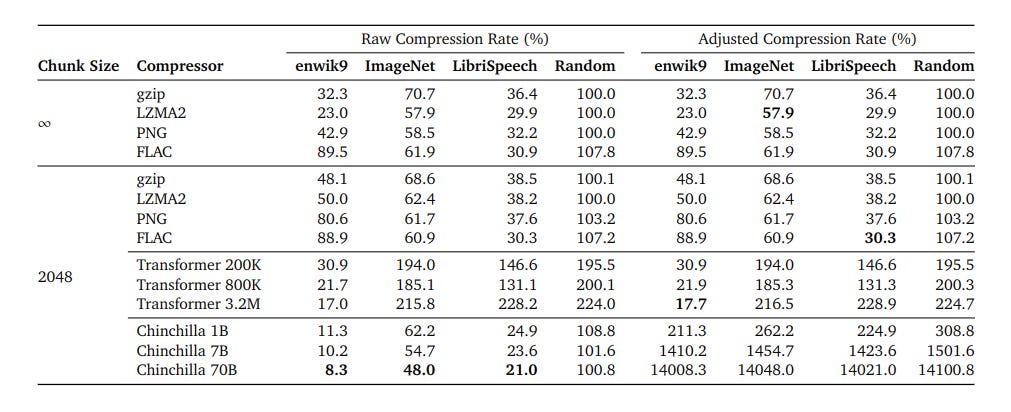
The authors found that in terms of raw compression rate, the Chinchilla 70B model achieves state-of-the-art compression rates on all three datasets. As enwik9 is part of Chinchilla’s training data, we expect it to be able to compress that dataset well. However, on ImageNet it achieved a raw compression rate of 48.0% beating PNG which achieved compression rate of 58.5%. Similarly, on LibriSpeech it achieved raw compression rate of 21.0%, beating FLAC (30.9%).

As far as the vanilla transformer models are concerned, they do not perform well on image and audio datasets. However, their raw compression rates are better than gzip and LZMA2 on enwik9 even though they were not trained on it.

Interpreting the Results

Let’s try to decode these results.

• Even though Chinchilla 70B can achieve state-of-the-art compression rates on data of different modalities, it cannot be used as a compressor in practical situations because of its size. The authors mention that it is not practical to use these models for compression unless we are compressing TBs of data.

• The main idea seems to be that the in-context learning ability of these large models allows them to learn the distribution of image or audio patches quite well, and they are able to predict the next bytes with high enough accuracy that it can be compressed effectively. In other words, this seems like an example of the in-context learning abilities of these models on image and audio data.

• The vanilla transformer model is not able to compress image and audio data, whereas the Chinchilla models are able to do that. Why is that—Is it because of the size difference, or the training data difference? The transformer models were trained only on the enwik8 dataset, whereas the Chinchilla models were trained on an internet scale dataset. The authors note that while it is unlikely that the Chinchilla training dataset contained the ImageNet and LibriSpeech data, however, it is possible their training data might have contained some image and audio samples encoded in the text.

Key Insight 2: Scaling Laws from the Point-of-view of Compression

Moving on to the second contribution from the paper—scaling laws and how they behave when viewed from the lens of compression.

Background on Scaling Laws

In their 2020 paper, Kaplan and his team found out that the scale of the neural language models significantly affects their performance. The model scale includes three factors: the number of model parameters (N), dataset size (D), and the training compute (C).

While Kaplan et al. list down a number of laws related to model scaling, we will concern ourselves with only the following two because the current paper reflects only on these two in the light of compression.

• Smooth Power Laws: Performance has a power-law relationship with each of the three scale factors N, D, C when not bottlenecked by the other two. These scaling trends cover a wide range but eventually flatten out.

• Universality of Overfitting: Performance improves predictably as long as we scale N and D together. Increasing one of the two factors while keeping the other fixed gives diminishing returns on performance. Performance penalty depends on the ratio N^0.74 / D, suggesting that 8x increase in model size requires a 5x increase in data.

Results on Scaling Laws

The authors evaluate the adjusted compression rate on the enwik datasets for the vanilla transformer models. They obtain the following graph (the axes are logarithmic).

Figure-2 from the paper showing adjusted compression rate of vanilla transformer of different sizes on enwik datasets

Based on this graph, the following observations are worth consideration:

• Larger models achieve better compression rates on larger datasets

• However, in case of smaller datasets, the compression rate quickly degrades as the model size increases. This is consistent with the scaling laws as laid out by Kaplan et al.

Interpreting the Results

In my view, there’s nothing really new here, except that even in terms of compression performance, the models follow the scaling laws. As we can see from the graph, increasing model sizes while keeping the dataset size fixed leads to deterioration in compression rates. This means that the models reached a plateau as far as their raw compression rate was concerned; however, due to increased model size, the adjusted compression rate shot up.

---

Key Insight 3: Effect of Context Window Size on Compression Rates

While general-purpose compressors such as gzip and LZMA depend on having a large context window in order to achieve effective compression rates, language models rely on a relatively short window. In this third experiment, the authors studied the performance of gzip, LZMA, vanilla transformer, and Chinchilla 1B on all three datasets by varying the size of the sequence lengths in their context window. They observed the following graphs:

Figure-6 from the paper showing compression rate for different models and algorithms on all three datasets by varying context window sizes

The authors note that the increased sequence length allows language models to achieve better in-context learning, thus leading to a quick decrease in compression rates.

Interpreting the Results

My interpretation of this result is that a larger sequence length in the model’s context allows the model to do better in-context learning. This is similar to providing more examples to the model in its context to help it learn the task better. As this improves the model’s prediction performance, it also leads to an improved compression rate.

Key Insight 4: Effect of Tokenization on Compression Rates

The final result from the paper worth discussing is the study of tokenization's effect on compression rates.

Background: Tokenization

Language models are not trained on raw text; instead, the text is broken down into smaller units (such as words or sub-words) called tokens. Each token is mapped to a unique integer ID, and the models are trained on those IDs. This naturally results in compression because long sequences of characters are being replaced by smaller integers. The total number of unique tokens created from the dataset becomes the vocabulary of the model.

There are different algorithms to do this, which decide how exactly the text should be broken down into tokens. The most common algorithm for doing this is called byte-pair encoding (BPE), which is the one evaluated in the paper.

Explaining how BPE algorithm works is beyond the scope of this article, but check out this article if you are interested in learning how it works: https://leimao.github.io/blog/Byte-Pair-Encoding/

Results

The authors compared the raw compression rates on enwik9 for the vanilla transformer model with different tokenizers: ASCII and byte-pair encoding (BPE) of different vocabulary sizes. They provide the following table in the paper, recording the raw compression rates obtained with different tokenizers:

Table-2 from the paper showing raw compression rate of vanilla transformer of different sizes by varying the tokenizer and vocabulary sizes

The authors make the following observations based on this experiment:

• Alphabet Size and Sequence Length: Increasing the alphabet or vocabulary size reduces the length of the sequence, which means more information is available within the model's context. However, this comes at a price—the task of predicting from a larger set of tokens becomes challenging.

• Effect of Model Size: The impact of token vocabulary size differs for smaller and larger models. Smaller models appear to benefit from a larger vocabulary size as it improves their compression rates. In contrast, larger models seem to experience a negative effect on the compression rate when the token vocabulary is expanded.

Interpreting the Results

In my view, the outcomes of this experiment are inconclusive and lack a definitive interpretation from the authors. All language models use some form of tokenization because it has been shown to improve the model's performance. However, in this experiment, it can be seen that for larger models, the compression rates deteriorate with an increased vocabulary size.

As the authors note that with an increased vocabulary, the task of prediction becomes challenging for the models because of larger number of tokens, that might explain why the compression rates of larger models become worse with a larger vocabulary. However, why don't smaller models suffer from this problem?

Also, as the paper is premised on the equivalence between prediction and compression, does this mean that there must be a similar level of negative impact on the predictive capabilities of larger models with an increased token vocabulary?

These questions seem to remain open from this experiment.

Final Thoughts

In summary, the paper “Language Modeling Is Compression” presents several interesting insights. It shows that large pre-trained language models, specifically Chinchilla 70B, can achieve remarkable compression rates on multi-modal datasets including not only text, but also image, and audio. This performance is potentially due to the model's impressive in-context learning abilities. However, questions remain as to whether the Chinchilla training dataset may have indirectly included ImageNet and LibriSpeech data.

The findings also align with scaling laws described by Kaplan et al., suggesting that expanding the model size when working with a fixed dataset initially improves the compression rate before causing it to deteriorate. Additionally, while increasing the vocabulary size improves compression rates for smaller models, the opposite is true for bigger models, which suggests larger models’ predictive capabilities might be negatively impacted with larger token vocabulary.

This article aimed to explain the complex ideas of the paper, in hopes of making them accessible to a wider audience. Enjoyed the discussion? Found the analysis insightful? Share your thoughts and conversations in the comments! I will be back with another intriguing topic in my next post.

---