How Unix Spell Ran in 64kB RAM

How do you fit a dictionary in 64kb RAM? Unix engineers solved it with clever data structures and compression tricks. Here's the fascinating story behind it.

Jan 12, 2025

This is the story of the design of Unix spell, how it was designed to perform spell checks by looking up an in-memory dictionary with just 64kB of RAM on the PDP-11. For reference, a typical dictionary consists of hundreds of thousands of words and 64kB memory can barely store a few thousand words.

This resource constraint led to an elegant system engineering story in Unix history. The final solution combined innovative linguistics, probabilistic data structures, and information theory to achieve what seemed impossible. More remarkably, it resulted in one of the earliest production uses of Bloom filters and an implementation of Golomb coding that achieved near-optimal compression ratios.

While modern spell checkers use different techniques like edit distance and language models, the engineering insights from Unix spell remain relevant. Even today, as we deal with terabyte-scale datasets on gigabyte machines, the fundamental challenge remains the same: how do we design efficient systems when resources are constrained?

This article not only explains how Unix spell worked within 64kB of memory but also shows the design process of arriving at such solutions through first-principles thinking.

TLDR;

If you're short on time, here's the key engineering story:

The Unix spell started in the 1970s as an afternoon prototype by Steve Johnson at AT&T, before Douglas McIlroy rewrote it to improve its performance and accuracy.
McIlroy's first innovation was a clever linguistics-based stemming algorithm that reduced the dictionary to just 25,000 words while improving accuracy.
For fast lookups, he initially used a Bloom filter—perhaps one of its first production uses. Interestingly, Dennis Ritchie provided the implementation. They tuned it to have such a low false positive rate that they could skip actual dictionary lookups.
When the dictionary grew to 30,000 words, the Bloom filter approach became impractical, leading to innovative hash compression techniques.
They computed that 27-bit hash codes would keep collision probability acceptably low, but needed compression.
McIlroy's solution was to store differences between sorted hash codes, after discovering these differences followed a geometric distribution.
Using Golomb's code, a compression scheme designed for geometric distributions, he achieved 13.60 bits per word—remarkably close to the theoretical minimum of 13.57 bits.
Finally, he partitioned the compressed data to speed up lookups, trading a small memory increase (final size ~14 bits per word) for significantly faster performance.

The rest of the article expands each of these points and gives a detailed explanation with all the math and logic behind them.

Origins of The Unix Spell Command

In order to secure funding for Unix, Ken Thompson and Dennis Ritchie pitched Unix as a text processing system for the patents department to AT&T. Naturally, a text processing system needed a spell checker as well.

The first version of Unix spell was written by Steve Johnson in 1975 which was a prototype. Jon Bentley mentions that Steve wrote it in one afternoon. Even though it worked, it was not very accurate.

It was pretty simple. It would split the input file into a stream of words, do some light preprocessing such as remove numbers and special characters, convert to lower case, then sort, unique, and finally pass the list to the spell program which would simply check for the existence of those words in a dictionary on the disk.

Because of its simplistic implementation, it was not very accurate, and also slow because of dictionary lookups on the disk.

After seeing the adoption of the initial version, Douglas McIlroy took up the project to rewrite it with the goal of improving the accuracy and performance of the tool. He worked on two separate fronts both involving some very clever engineering:

Building an affix removal algorithm for reducing words to their stems, and a compact dictionary consisting of the stem words
A compact data structure for loading the dictionary into memory for doing fast lookups

This article is going to be focused on the data structure design part, but let’s spend a section to get an overview on the affix removal algorithm to see how it worked.

The Affix Removal Algorithm

Using a full fledged dictionary for doing lookups was slow because the computers those days had only a few kilobytes of main memory and using disk based lookups was even more slower.

Douglas McIlroy came up with the idea of an algorithm which would iteratively remove common prefixes and suffixes from a word and look up a dictionary to see if the reduced word is present in it or not. The algorithm would follow the affix removal process until there were no affixes left to remove and if even after this the word was not present in the dictionary, then it would be flagged as a misspelling.

For instance, the algorithm would reduce the word “misrepresented” to “present” by removing the prefixes “mis”, “re”, and the suffix “ed”. And because “present” is a valid word in the dictionary, it would not flag it as a misspelling.

This affix removal technique was not 100% accurate and would sometimes let misspelled words pass through. For instance, “appled” would not be caught by it because after removing the “ed” suffix, “apple” would be a valid word. But such occurrences were deemed acceptable at that time. He also implemented a bunch of exceptions to these rules to avoid some of the common errors.

Overall, this algorithm resulted in a very compact dictionary. The final dictionary consisted of 25,000 words, which seemed possible to load into memory with a well engineered data structure.

Let’s move on to discussing how he managed to implement in-memory dictionary lookups with just 64 kB of memory.

A Bloom Filter based Lookup

Bloom published his work on Bloom filter in 1970 while the Unix spell was developed in the mid-1970s. At this time, Bloom filter was not even called Bloom filter. In his paper, Douglas calls it a “superimposed code scheme”.

Interestingly, the Bloom filter implementation he used was given to him by Dennis Ritchie.

Even though the dictionary size was 25,000 words, it was still not possible to load it as it is in just 64kB of RAM. Besides, it also needed fast lookups.

The first data structure that Douglas used was a Bloom filter. In the paper he doesn’t call it Bloom filter, instead he refers to it as a “superimposed coding scheme”, attributed to Bloom’s paper from 1970. Interestingly, he gives the credit for the implementation of the Bloom filter he used to Dennis Ritchie.

A Bloom filter consists of a bit table initialized to all zeros. To add an item to the Bloom filter, you apply multiple hash functions to the item. Each hash function generates an index in the table, and that bit index is set to 1. If k hash functions are used, then, k different bit indices are turned on in the table.

For a more detailed explanation of Bloom filter, please check out my article on Bloom filters.

Looking up an item, whether it exists in the table or not, requires the same procedure. You need to apply the k hash functions, and for each of them check if the corresponding bit is set to 1 in the table or not. If even one of the bits is not on, then it means that the item is not present in the dataset. However, if all the bits are set, then it indicates that the item might be present, but this may also be a false positive.

False positives can occur because of hash collisions. When querying for an item, we cannot be 100% sure if a bit is on in the table because of the query item, or because of a hash collision with another item.

When using Bloom filter, you need to implement a strategy to handle false positives. For instance, in this case it could mean doing a full dictionary search. But that would defeat the whole purpose of using a Bloom filter, which was to save memory and do fast dictionary lookups. In the case of a spell checker, most of the words exist in the dictionary and only a fraction of words are misspelled, so we would be checking the full dictionary quite a lot.

However, a Bloom filter can be tuned to achieve a desired false positive rate. The following formula computes the false positive probability for a Bloom filter with a given size n, number of inserted items m, and number of hash functions k.

$\begin{align*} &\text{q} \approx \left( 1 - e^{-\frac{kn}{m}} \right) \\ &\text{where:} & \\ &\text{q}:\ \text{Probability that a bit is 1} \\ &m: \ \text{Number of bits in the Bloom filter} \\ &k: \ \text{Number of hash functions used} \\ &n: \ \text{Number of elements inserted} \end{align*} $

In his paper, Douglas mentions that a false positive probability of 1 in 2000 was acceptable to them, which meant that for such a low false positive rate, they did not need to consult the dictionary.

As they had a dictionary of 25,000 items, the number of items was fixed. They fixed the bit table size at 400,000 bits because of the limited amount of memory. Based on these factors, using 11 hash functions allowed them to keep the false positive rate at around 1/2000.

Results of Using Bloom Filter

They used the Bloom filter based spell implementation for a while. In the paper, Douglas mentions that even though the false positive rate was acceptable, in the wild, they were encountering a lot of new words that needed to be added to the dictionary. This led to the dictionary size going up from 25,000 to 30,000.

However, for a dictionary of this size, their Bloom filter required a bigger bit table size which was not possible for them. As a result, Douglas looked for alternate data structure designs to be able to fit a dictionary of 30,000 words in memory with similar lookup performance and accuracy.

A Compressed Hashing Scheme for Dictionary Lookups

As the dictionary size exploded from 25,000 to 30,000, Douglas needed a more memory efficient data structure to hold the dictionary in memory.

A hash table was an attractive solution, but it would have consumed much more memory than a Bloom filter because it requires storing the hash, as well as, the actual words to handle collisions.

Instead of a full hash table, Douglas decided to store just the hashes of the words. The lookup required computing the hash of the input word, and then checking for its existence in the hashes using a scan.

One intuition for doing so might have been that the individual words can be of varying lengths, but a hash function will naturally compress them down to a fixed number of bits, and that may possibly allow them to fit the hashes in memory.

But hashes can collide, so they needed a large enough hash code to have an acceptably low probability of collisions.

Computing the Optimal Hash Code Size

If each word in the dictionary is hashed to a hash code of size b bits, then there are 2^b total possible hash codes in that space. If the size of the dictionary is v words, then the probability of a hash collision can be computed as:

$\begin{align*} \text{P(hash collision)} = \frac{v}{2^b} \end{align*}$

They had a dictionary of 30,000 words, which is ~2^15 words. Moreover, he mentions that a collision probability of 1 in 2^12 was acceptable to them. This gave a hash code size of 27 bits.

But 27-bit hash codes were too big: with 2^15 words, they needed 2^15 * 27 bits of memory, while the PDP-11 had only 2^15 * 16 bits (64kB) of RAM—compression was essential.

The Theoretical Minimum Limit of Hash Code Compression

Before implementing any compression algorithm, we need to know what is the theoretical minimum number of bits we can achieve to compress this piece of data. It acts as a benchmark to tell us how well we are able to compress the data.

This theoretical minimum is computed using the information content of the event which generated the data we are trying to compress. This concept comes from information theory which is the underpinning foundation for all of the data compression techniques.

Information Content of an Event

The basic idea behind information content is to use the probability of an event to determine how many bits are needed to encode it without loss of information.

A highly likely event carries less information (for instance a 100% probable event has no information and needs 0 bits to encode), while a less probable event contains much more information and needs more bits. There is an inverse relationship between the probability of an event and its information content, which leads to the following formula:

$\begin{align*} &\text{I(E)} = \log_2\left(\frac{1}{P(E)}\right) \\ &\text{Or, I(E) = } -\log_2{P(E)} \\ &\text{where P(E) is } \text{probability of event E} \end{align*}$

Now, to compute the information content of a set of hash codes, we need to figure out the probability of generating them.

If the size of a hash code is b bits, then there are a total of 2^b possible hash codes in that space. Out of that, we are selecting a set of v unique hash codes.

$ \begin{align*} \text{The total number of ways to select such sets = }\binom{2^b}{v} \end{align*} $

Therefore, the probability of any one of these sets of being generated is:

$\begin{align*} \text{P} = \frac{1}{\binom{2^b}{v}} \end{align*} $

Thus, the information content of these hash codes is:

$\begin{align*} &I(E) = - \log_2\left(\frac{1}{\binom{2^b}{v}}\right) \\ &= \log_2\left(\binom{2^b}{v}\right) \\ &= \log_2\left(\frac{(2^b)!}{v! \, (2^b - v)!}\right) \end{align*}$

To simplify things, we can use Stirling’s approximation:

$\begin{align*} &\text{Stirling's approximation: } \quad \log_2(n!) \approx n \log_2(n) - n \log_2(e), \\ \end{align*} $

The paper makes another simplifying assumption that the number of words in the dictionary (30,000) is much smaller than the total number of hash codes (2^27), i.e., v « 2^b, this allows them to simplify (2^b - v) as 2^b in the above computation.

Using these two approximations leads to the following formula for the information content:

$\begin{align*} &I(E) \approx v\left[b - \log_2\left(\frac{v}{e}\right)\right] \end{align*}$

Plugging in v=30,000 and b=27, the minimum number of bits needed to encode a single hash code turns out to be 13.57, which was ~50% shorter than the original hash codes, and within the capacity of the PDP-11’s memory.

A Delta Based Compression Scheme

At this point they knew how much compression they could achieve but the bigger question was how to get there. Instead of compressing the raw hash codes, what if they computed and stored the differences between successive hash codes (in their sorted order)? This is similar to how delta encoding works, but not quite the same.

There were a couple of advantages of working with hash differences.

By definition the differences were smaller than the raw hash codes
And many of the difference value would repeat because the difference of several hash codes might be the same.

This implied that it was easier to compress these differences than the hash codes.

Computation of Hash Differences

Hash differences were computed by sorting the hash codes and taking differences between consecutive values.

For instance:

sorted hash codes: 5, 14, 21, 32, 55, 67
hash differences: 5, 9, 7, 11, 23, 12

Let’s also see how the lookup of a word worked when they stored hash differences instead of the actual value.

Looking Up a Word for Existence

To check if a word exists in the dictionary or not, they would compute the hash of the word and check for its existence in the dictionary via a simple algorithm.

lookup(input_hashcode) -> bool:
  sum = hash_differences[0]
  i = 1
  while True:
    sum += hash_differences[i]
    if sum == input_hashcode:
      return True
    if sum > input_hashcode:
      return False
    i += 1

Now, let’s discuss how they came up with a compression scheme for this data.

Mathematical Modelling of the Hash Code Differences

The basic principle behind lossless compression is to assign shorter codes to symbols with higher probabilities, and longer codes to symbols with lower probabilities. This makes sense because symbols with higher probabilities tend to occur more frequently in the data and assigning them shorter codes means higher compression rate.

But this requires computing the probability distribution of all the symbols in the data, and then using it to generate compressed codes. The probability distribution table is needed at decompression time as well to perform the decoding.

This had two problems for Douglas:

Holding a probability distribution table for ~30,000 symbols in memory would have taken away any compression advantage he was getting from compression itself. So he needed a scheme which was free of this requirement.
Computing the probabilities of the hash differences would have been time expensive. All the 30,000 possible hash difference values, their sums and counts would not have been possible to keep in memory for computing their probabilities. So, it would have required an expensive disk based data structure to compute these probabilities.

But McIlroy came up with an elegant solution by recognizing that the hash differences followed a geometric distribution, enabling an efficient compression scheme. Let’s first understand how these hash difference values are geometrically distributed.

Modelling of the Hash Differences as a Geometric Distribution

The geometric distribution is a discrete probability distribution which is used to model scenarios where we conduct an experiment until we get a success. For instance, rolling a six-faced die until we get a “1” forms a geometric distribution, with the probability of success being 1/6. A simpler example is tossing a coin until we get a head.

If the probability of failure is p, the probability of success is q, and if success occurs in the kth trial, then the probability mass function of the geometric distribution is given by the following formula:

$\begin{align*} &P = p^kq \end{align*}$

Now, let's understand how the hash difference values map to this distribution.

As each hash code is b bits wide, we have a space of 2^b points. And we have v hash codes spread out in this space. The probability of any point in this space containing a hash code is q=v/2^b, and the probability of a point being empty is p=1-(v/2^b).

$\begin{align*} &\text{P(a point containing a hash code)} = q = \frac{v}{2^b} \\ &\text{P(an empty point)} = p = 1 - \left(\frac{v}{2^b}\right) \end{align*}$

But we are interested in modelling the distribution of hash difference values, rather than the hash codes themselves. A hash difference k occurs when two consecutive hash values in the sorted sequence are k positions apart. For instance, if we have two successive hash code values 20 and 25, then the hash difference is 5.

What's the probability of seeing a hash difference of k? Given any hash value h in our space:

We need the next k-1 positions after h to be empty
And then we need a hash value at position h+k
The probability of k-1 empty positions is p^(k-1)
The probability of a hash value at position h+k is q

Therefore, the probability of a hash difference of k is:

$\begin{align*} &\text{P(difference=k) =} p^\left(k-1\right)q \end{align*}$

This follows exactly the form of a geometric distribution!

If you read the spell paper, you will find that the author takes a different route to arrive at this conclusion. He models the generation of the hash codes as a Poisson process and proceeds from there.

But, what is the point of modelling this as a geometric distribution? It turns out, there is a very simple and efficient run-length encoding scheme for geometrically distributed integers given by Golomb in his 1965 paper. Let’s see how it works.

A Compression Scheme for Geometrically Distributed Integers (Golomb’s code)

Golomb’s code is a simple run-length encoding scheme for geometrically distributed integers which was used by Douglas to compress the hash differences. It takes advantage of the fact that geometrically distributed values have an exponentially decaying probability of success, which can be leveraged for performing compression.

What do we mean by that? Recall that in the case of geometric distribution, the probability of success after k trials is given as:

$P = p^kq$

Let’s say, we find an integer m, such that p^m = 1/2. Then, it means that the probability of success after k + m trials is:

$\begin{align*} &\text{P(success after k + m trials)} = p^\left(k + m\right)q = \frac{1}{2}p^kq \end{align*}$

In other words, the probability of getting success in k + m trials is half of that of the probability of getting a success in m trials. And this probability continues to half every m successive trials. This is an exponentially decaying distribution of probabilities.

Understanding Exponentially Decaying Probabilities with Example

Let's consider a fair coin toss example where we toss the coin until a head occurs. For a fair coin, p = q = 1/2.

Here, we have m = 1, because p^1 = 1/2. It means that the probabilities decay by half every trial:

$\begin{align*} &P(k=1) = \frac{1}{2} \\ &P(k=2) = \frac{1}{4} \\ &P(k=3) = \frac{1}{8} \\ &P(k=4) = \frac{1}{16} \end{align*}$

Let’s take another example of a biased coin, such that p=1/sqrt(2) = 0.707, and q=0.293.

Here, we have m=2, because p^2 = 1/2. In this case the probabilities decay after blocks of size 2.

$\begin{align*} &P(k=1) = 0.293 \\ &P(k=2) = 0.207 \\ &P(k=3) = 0.116 \\ &P(k=4) = 0.104 \\ &P(k=5) = 0.073 \\ &P(k=6) = 0.051 \end{align*}$

You can see that the probabilities decay by half for every even value of k. For instance:

$\frac{P(k=2)}{P(k=4)} = \frac{P(K=4)}{P(k=6)} \approx 0.5$

Significance of Exponentially Decaying Probabilities

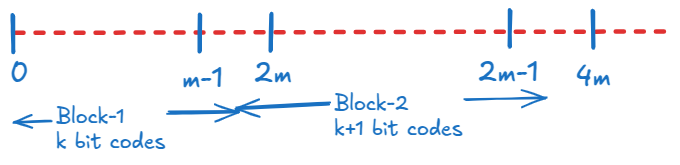
This pattern of exponential decay allows us to group the hash difference values in blocks of size m. Each value within a block gets a code of size k bits, while the next block gets codes of size k + 1 bits. The reasoning behind it is rooted in information theory.

The minimum number of bits required to encode the outcome of an event is given by its information content which is -log₂(p), where p is the probability of that event.

It means that if an event has probability 1/2, it needs 1 bit code, an event with probability 1/4 needs 2 bits, an event with probability 1/8 needs 3 bit codes and so on.

We can leverage this for geometrically distributed values by arranging them in blocks of size m. The values within a given block can be assigned codes of equal length, and the values in the subsequent block gets codes one bit wider for its m values.

Arranging hash code differences in blocks of sizes m, where each block’s probability is half of that of its predecessor. If the predecessor block gets k bit wide codes, the next block gets k+1 bit wide codes.

It turns out, formation of blocks with increasingly larger codes also leads to a beautiful self-similar bit pattern with properties that make it very easy to generate such codes. Let’s see how this self-similar pattern forms.

Self-Similar Patterns

Self-similar pattern essentially means that the codes at a specific index within a block repeats itself at the same index in the next block, with one padding bit added on its left.

For instance, if the code at the 2nd position in the first block is 0001, then the 2nd code in the 2nd block will be 10001. Similarly, the 2nd position code in the 3rd block will be 110001, and so on.

This self-similar pattern naturally emerges because of the enforcement of 1 bit longer codes in each successive block. Let us see a concrete example.

Example of Self-similar Codes

Let’s say, our block size is m=5 and the codes in the first block are k=4 bits wide.

If the first code in the first block is 0110, then we can generate the codes for the rest of the block by adding 1 to the previous code value. The codes for the first block will look like this:

block-1 codes: 0110 0111 1000 1001 1010

As you can see, the first block ends at the code 1010. The natural value for the next code should be 1011, but because this code lies in the next block, its code has to be 1 bit larger. As a result we need to left shift it by one bit, which makes it 10110. And if you notice the least 4 bits of this code are the same as the first code in the first block. The following diagram highlights this visually.

An example of self-similar codes. The first code in the first block are same as least 4 bits of the first code in the 2nd block

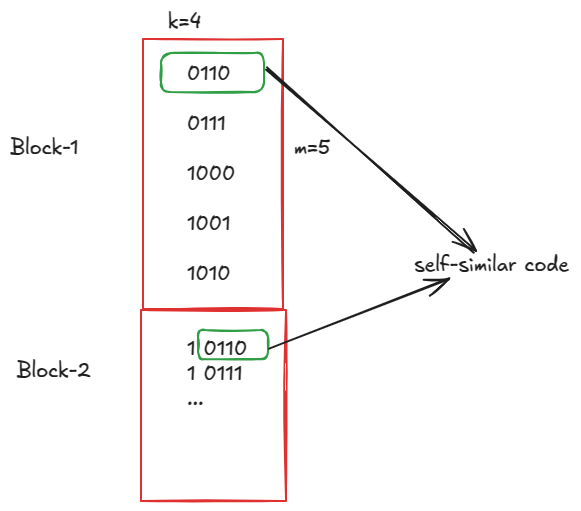
Another thing worth Noticing here is that we are obtaining the first value of the 2nd block by left shifting it by 1 bit, which means its least significant bit (LSB) is always 0. 

For the self-similar patterns to form, the first code of the first block should also always have its LSB set to 0. This implies that this first code is always an even number of the form 2x.

The self-similar code has a couple of additional properties which provide an intuitive way to figure out the minimum bit width k for the codes in the first block. Let’s see how.

Bit Width of the Codes

To figure out the minimum number of bits needed to encode the first block, let’s assume the first encoded value in the first block is 2x.

Then the first code of the 2nd block should be 2x + m. However, because the codes in the next block need to be 1 bit wider, this value gets shifted to the left by 1 bit, which makes it 2(2x + m).

Left shifting a value by 1 bit doubles it.

The self-similarity pattern gives rise to another way to think about these codes. If the first code in the first block is 2x, then in the next block:

We want the same pattern (2x)
But with an extra bit on the left
Adding a bit on the left is equivalent to adding 2^k
So the code becomes 2^k + 2x

Combining these two relations gives us the following equation

$\begin{align*} &2^k + 2x = 2(2x + m) \\ &\text{Or, } 2^k = 2m + 2x \\ &\text{Here, x is a nonnegative integer, so we can simplify the above to:} \\ &2^k \ge 2m \end{align*}$

By solving for the smallest integer value of k we can get the code width of the first block.

The same equation also gives us the value of x:

$\begin{align*} x = 2^\left(k-1\right) - m = 2^{\log_2(m)} - m \end{align*}$

Knowing the values of m, k, and x gives way for a simple encoding algorithm.

The Encoding Algorithm

The paper by Golomb gave a different algorithm for encoding and decoding, but the Unix spell code used a slightly complicated but more efficient algorithm. I describe the algorithm as implemented in the Unix spell.

Let’s understand how to encode a value using Golomb’s code. Recall that we have:

Initial bit width k
Block size m
First code in first block is 2x, where x = 2^(k-1) - m

Here’s the encoding algorithm:

def encode(value):
    # Case 1: Values less than x
    # These get shorter codes of length k-1
    # Because we have unused bit patterns available
    if value < x:
        return value, k-1  # return (code, length)
    
    # Case 2: Values >= x
    # Need to find which block they belong to
    value = value - x     # adjust relative to first code
    y = 1                 # tracks block number through bit shifts
    length = k           # start with k bits
    
    # Find block by repeatedly subtracting block size
    while value >= m:    # m is block size
        value -= m       # move to next block
        y = y << 1      # add padding bit for next block
        length += 1     # each block needs one more bit
    
    # Generate final code:
    # (y-1) << k creates padding bits based on block number
    # x*2 adds offset for the first code
    # value adds position within current block
    code = ((y-1) << k) + (x*2) + value
    return code, length

The following figure shows two examples to illustrate how it works in practice:

Examples of how the encoding algorithm works for values 2 and 8

You can find the original Unix svr4 implementation of this algorithm here.

The Decoding Algorithm

The decoding process is also not that complicated. Given a code, we need to:

First look at its top k-1 bits (call this w):
- If w is less than x, then this is a shorter code
- The decoded value is simply w itself
If w ≥ x, then we need to
- Include one more bit into w
- Look at the least significant k bits of w: call it u
- if u < 2x + m:
  - value = x + u + (s - 1)m
  - where s is the number of extra bits included into w
- else:
  - keep including more bits into w until u < 2x + m

You can find the original Unix svr4 implementation of the decode algorithm here.

The Compression Efficacy of Golomb Codes

So how well this technique was able to compress the hash differences?

Recall that the theoretical limit of compression was 13.57 bits per word. Golomb codes managed to achieve an expected code length of 13.60, remarkably close to this theoretical minimum.

However, looking up a value in this compressed dictionary was quite slow. It required starting from the beginning, decoding and summing values until finding or exceeding the desired hash code.

To speed this up, the final Unix spell implementation partitioned the table of differences into M bins. This allowed them to first locate the correct bin, and then only scan within that bin, speeding up the search by a factor of M.

This partitioning scheme required storing additional pointers to the bins, adding log₂M bits per word to the storage requirement. The total storage increased to about 14 bits per word, but this was an acceptable trade-off: it was still within their memory budget while providing significantly faster lookups.

Conclusion

The Unix spell command is a fascinating piece of engineering history that emerged from the severe memory constraints of the PDP-11. What makes it particularly interesting is how it evolved from a simple disk-based dictionary lookup to an elegant solution combining multiple computer science concepts:

Probabilistic data structures (Bloom filters)
Information theory (optimal bit width calculations)
Probability theory (geometric distribution)
Compression algorithms (Golomb coding)

The engineering journey is particularly instructive:

Started with Bloom filters achieving acceptable false positive rates
When dictionary size grew, switched to compressed hashing where:
- They computed theoretical minimum bits needed
- Recognized patterns in hash differences
- Used Golomb's code to achieve near-optimal compression
- Added binning for faster lookups with minimal space overhead

Even though modern spell checkers use different techniques like edit distance and language models, the engineering insights from Unix spell remain valuable. It shows how deep understanding of theoretical concepts combined with practical constraints can lead to efficient and elegant solutions.

Most importantly, it demonstrates that some of the best innovations happen when we are resource constrained, forcing us to think deeper about our problems rather than throwing more hardware at them.

References

Support Confessions of a Code Addict

If you find my work interesting and valuable, you can support me by opting for a paid subscription (it’s $6.40 monthly/$58 annual). As a bonus you get access to monthly live sessions, and all the past recordings.

Subscribed

Many people report failed payments, or don’t want a recurring subscription. For that I also have a buymeacoffee page. Where you can buy me a coffee or become a member. I will upgrade you to a paid subscription for the equivalent duration here.

Buy me a coffee

I also have a GitHub Sponsor page. You will get a sponsorship badge, and also a complementary paid subscription here.

Sponsor me on GitHub