Understanding DeepMind's AlphaDev Breakthrough in Optimizing Sorting Algorithms

A Comprehensive Analysis of AlphaDev's Performance and Effects on Small Sorting Tasks

Jun 10, 2023

Introduction

Last week DeepMind published a paper in Nature showcasing a breakthrough in using deep reinforcement learning to optimize the performance of small sorting algorithms. Their AlphaDev model discovered improved sorting routines by playing a game and managed to surpass previously known human benchmarks for certain sorting tasks. This paper caught my eye as I wanted to understand exactly what optimizations did the model find. Although, the paper is very detailed, it spends little time in explaining the solutions found by the model. As someone who does not code in assembly language, I had to spend sometime to see why the program generated by AlphaDev was correct. I am sure, there must be many people like me who might be interested in this, so here we are. This article will explore the algorithms discovered by AlphaDev in detail to make this discovery accessible to a wider audience. While the focus will be on the algorithmic optimizations, the article will not cover the model design or training aspects of AlphaDev.

Why Optimize Small Sorting Algorithms?

Sorting is an essential operation executed trillions of times daily, and even minor improvements can lead to significant performance boosts in software stacks across the industry. In their study, DeepMind focused on optimizing fixed small-sized sorting algorithms, such as sort 3, sort 4, and sort 5. There are two main reasons for this focus:

As the sequence to be sorted becomes larger, the number of steps required to find the correct solution grows rapidly.
General sorting algorithms (such as quick sort and merge sort) repeatedly call fixed-length sorting functions internally to sort smaller arrays, so optimizing these smaller sorting functions can enhance the performance of larger sorting tasks. In their paper, DeepMind notes that such fixed length sorting routines are executed trillions of times every day. So even a small performance improvement can easily add up in massive efficiency gains.

sort n basically refers to a routine to sort a fixed list of n numbers

AlphaDev's Learning Approach

DeepMind used deep reinforcement learning to train this model. Deep reinforcement learning is a type of machine learning technique which involves an agent learning to make sequential decisions in an environment in order to achieve a goal. By receiving rewards or penalties for its actions and attempting to maximize cumulative rewards, the model learns to solve tasks.

In this work, DeepMind have named their learning agent as AlphaDev. AlphaDev is designed to play a game called AssemblyGame, where its goal is to generate assembly language instructions to sort a set of numbers. The agent takes action by generating an assembly language instruction which gets appended to the list of instructions generated by it in the game so far. The agent is rewarded or penalized based on two factors: 1) the algorithm correctness, and 2) the latency. The latency reward can be computed by either penalizing the agent for increasing the length of the program (when the length of the program is closely correlated with its latency) or by actually measuring the latency of the program. The agent wins the game by generating a correct and low latency assembly language program.

AlphaDev's Performance on Sorting Tasks

The authors ran the model on three sorting problems: sort 3, sort 4 and sort 5. The benchmark algorithms for these problems are based on sorting networks, which generate optimized conditional branchless code for sorting such fixed set of numbers. According to the paper, the AlphaDev agent outperformed the benchmark for sort 3 and sort 5 algorithms by reducing one assembly instruction in its generated program. For sort 4, it achieved the same performance as the benchmark.

Branchless code in general is very fast. The CPU tries to do branch prediction when it sees a branching instruction (think if-else conditions in your code), and tries to execute the code in the predicted branch ahead of time for maximum efficiency. However, if it ends up with a wrong prediction, not only all that extra work is wasted, but now the code in the other branch needs to be executed. On top of that, branching usually involves jump instructions. Too much jump around can badly affect the performance, as opposed to linear code execution.

What is a Sorting Network

In the paper DeepMind used sorting networks as the benchmark algorithms. A sorting network is an abstract device which consists of two components: wires, and comparators. Wires carry values (one value per wire) from left to right, and comparators connect any two wires. The values traverse the wires all at the same time, and when they encounter a comparator, the wires connected by the comparator exchange their values, if and only if the top wire’s value is greater than or equal to the bottom wire’s value. As the values finish traversing the network, the maximum value shifts to the bottommost wire and the smallest value shifts to the topmost wire, thus resulting in a sorted network.

A sorting network of 4 wires and 5 comparators

For a given set of wires, there can be a large number of possible sorting networks that can be constructed. However, for the sort 3, sort 4 and sort 5 problems, the most optimal sorting networks are well known, which have been used as the benchmark in the DeepMind paper.

Benchmark vs. AlphaDev's Optimized Sort 3 Algorithm

We will start by looking at the benchmark algorithm of sort 3 problem, where the requirement is to sort a fixed list of 3 numbers. The optimal human benchmark for sort 3 is a sorting network as shown below (picture taken from the paper itself).

The circled part receives three inputs, A, B, and C, and transforms them in sorted order as its output. The authors note that the comparator before the circled part ensures that the following inequality always holds:

\(B \leq C \)

In programming terms, this basically means that B and C were already known to be sorted before this routine even began. We will use this inequality when we prove the correctness of the program.

Now, let’s look at the pseusdocode of the benchmark assembly program for sorting 3 numbers A, B, C:

Memory[0] = A
Memory[1] = B
Memory[2] = C

mov Memory[0] P
mov Memory[1] Q
mov Memory[2] R
mov R S // S = C
cmp P R // compare A and C
cmovg P R // R = max(A, C)
cmovl P S // S = min(A, C)
mov S P // P = min(A, C)
cmp S Q // compare min(A, C), B
cmovg Q P // P = min(A, B, C)
cmovg S Q // Q = max(min(A, C), B)

mov P Memory[0] // min(A, B, C)
mov Q Memory[1] // max(min(A, C), B)
mov R Memory[2] // max(A, C)

This is very similar to x86 assembly syntax. If you are not familiar with it, here’s the short guide just enough to explain the above code.

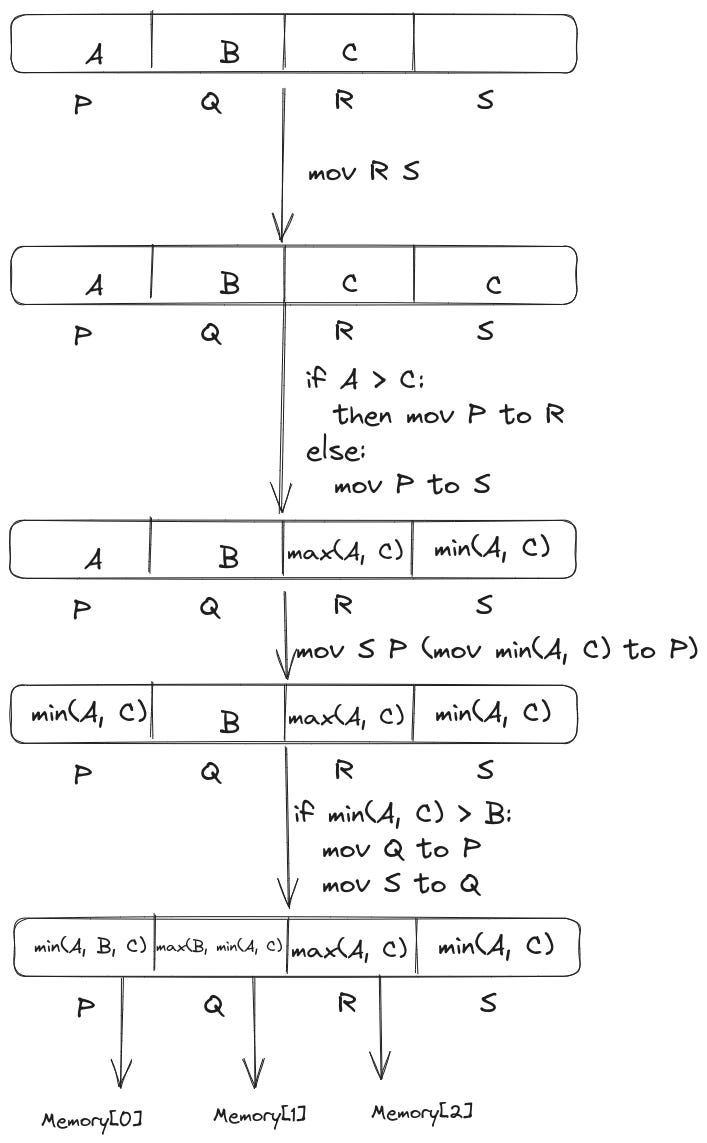
A quick rundown of the assembly instructions used in the programs in this article

The following diagram shows how the registers are modified through the different steps of the benchmark sort 3 algorithm.

Visual depiction of the registers through the various steps of the algorithm

Even though, this looks complicated but the underlying logic is pretty simple. First, we compare A and C, to find min(A, C) and max(A, C).

Next, we compare B and min(A, C), to find min(A, B, C) and max(B, min(A, C)).

The above two operations lead to the following final state of the registers:

P = min(A, B, C)
Q = max(B, min(A, C))
R = max(A, C)

Let’s verify if this is sorted or not:

The register P obviously contains the smallest value. In addition to that, we know that B <= C (the sorting network guarantees this, see the note below the sorting network diagram at the beginning of this section). Therefore, min(A, B, C) is equivalent to min(A, B).

Now, we have two cases to follow.

if A < B then:
- P = A (the smallest value)
- Now, as B <= C and A < B, therefore A < C and min(A, C) = A
- Q = max(B, min(A, C)) becomes B (the 2nd smallest value) because min(A,C) = A and B > A
- Finally, R is left with C, which is the largest value
Else, if A > B then:
- min(A, B) = B (the smallest value)
- Q = max(B, min(A, C)) becomes min(A, C) because we know that B is the smallest value
- and R = max(A, C) contains the largest value.

Thus, we can see that the algorithm indeed results in sorted numbers.

AlphaDev’s Optimized Algorithm for Sort 3

Now, let’s take a look at the optimized algorithm discovered by AlphaDev for the sort 3 problem.

Memory[0] = A
Memory[1] = B
Memory[2] = C

mov Memory[0] P
mov Memory[1] Q
mov Memory[2] R
mov R S // S = C
cmp P R // compare A and C
cmovg P R // R = max(A, C)
cmovl P S // S = min(A, C)
mov S P // P = min(A, C) // AlphaDev removed this mov
cmp S Q // compare min(A, C), B
cmovg Q P // P = min(A, B)
cmovg S Q // Q = max(min(A, C), B)

mov P Memory[0] // min(A, B)
mov Q Memory[1] // max(min(A, C), B)
mov R Memory[2] // max(A, C)

The algorithm is almost identical to the benchmark algorithm that we saw earlier, with just one difference. AlphaDev figured out that the highlighted mov S P instruction was unnecessary and it did not generate it in its optimized version of the algorithm.

Without that mov instruction, the value of P remains as A when the cmp S Q instruction is executed. We need to ensure that even without the mov instruction, the final values in P, Q and R are sorted.

Let’s analyze the following three lines of the algorithm and ensure that they are still correct even after the removal of the mov before them.

cmp S Q // compare min(A, C), B
cmovg Q P // P = min(A, B, C)
cmovg S Q // Q = max(min(A, C), B)

cmp S Q compares the values min(A, C) and B. We need to verify that even without the mov S P instruction, the registers P and Q still end up with the values min(A, B, C) and max(min(A, C), B) respectively. There are two possible outcomes of comparing min(A, C) and B. We will consider both of them in order.

If B < min(A, C) then:
- we store B in P which is equivalent to min(A, B, C).
- we set Q with value min(A, C) which is same as max(min(A, C), B) since min(A, C) > B
Else, if B > min(A, C) then:
- In this case, P contains the value A. Is that equivalent to min(A, B, C)? We know that B <= C and B > min(A, C), therefore B > A. In other words A < B <= C. Thus, min(A, B, C) = A.
- Next, let’s verify that Q contains the right expression. In this case, Q contains the value B. Is that the same as max(min(A, C), B)? We know that B <= C and B > min(A, C). Therefore max(min(A, C), B) = B.

This shows that even in this optimized algorithm, the registers P, Q, and R end up with the same output as the benchmark algorithm.

In the paper, the authors call the elimination of the extra mov instruction as the AlphaDev Swap Move.

Benchmark vs. AlphaDev's Optimized Sort 4 Algorithm

Next, let’s take a look at the optimized algorithm found by AlphaDev for sorting a fixed set of 4 numbers.

Benchmark for Sort 4 Algorithm

In the paper, the authors showed a sort 4 sorting network as the most optimal algorithm for sorting 4 numbers. They used a configuration that is part of a larger sort 8 sorting network. The network configuration is shown below, taking four inputs A, B, C, D, and transforming them into four outputs. As this configuration is part of a larger sort 8 network, by the time the input reaches it, the following inequality holds true:

\(D \geq \min(A, C) \)

Now, let's take a look at the pseudocode for the implementation of the above-shown network.

Memory[0] = A
Memory[1] = B
Memory[2] = C
Memory[3] = D

mov Memory[0] P // P = A
mov Memory[1] Q // Q = B
mov Memory[2] R // R = C
mov Memory[3] S // S = D

cmp S P // compare D vs A
mov P T // T = A
cmovl S P // P = min(A, D)
cmovl T S // max(A, D)

cmp R P // compare C vs min(A, D)
mov P T // T = min(A, D)
cmovg R P // P = max(C, min(A, D))
cmovl R T // T = min(A, C, D)

cmp Q T // compare B vs min(A, C, D)
mov T U // U = min(A, C, D)
cmovl Q U // U = min(A, B, C, D)
cmovl T Q // Q = max(B, min(A, C, D))

mov U Memory[0] // min(A, B, C, D)
mov Q Memory[1] // max(B, min(A, C, D))
mov P Memory[2] // max(C, min(A, D))
mov S Memory[3] // max(A, D)

This algorithm is very similar to the sort 3 algorithm.

First we compare A and D to find min(A, D) and max(A, D).
Next, we compare C and min(A, D) to find min(A, C, D) and max(C, min(A, D)).
Finally, we compare B and min(A, C, D) to find min(A, B, C, D) and max(B, min(A, C, D)).

Let’s verify if this results in sorted output or not

We know that min(A, B, C, D) is the smallest value.

However, we also know that D >= min(A, C).

Therefore, min(A, B, C, D) is same as min(A, B, C).

This means that one of the three: A, B, C could be the minimum value. We have to assume one of them as the minimum and verify that the other expressions result in the next three smallest values.

Let’s assume A is the minimum value, i.e. A < B and A < C.

We know that D >= min(A, C), therefore D >= A as well.

With this knowledge, let’s verify if max(B, min(A, C, D)) is the 2nd smallest value.

min(A, C, D) = A as we have assumed A is the minimum value. Therefore the expression max(B, min(A, C, D))becomes max(B, A), which is equal to B.

For the 3rd smallest value, we have the expression max(C, min(A, D)).

This is same as max(C, A) because D >= A. As A < C, max(C, A) = C which is our 3rd smallest value.

Finally, for the 4th smallest value we have the expression max(A, D) which becomes D since we know that D >= A.

We can repeat the above process for B and C as the smallest values and verify that the four expressions still lead to the sorted outputs. I will not do that here to save space.

Optimized Sort 4 Algorithm

Let’s see the algorithm discovered by AlphaDev for the sort 4 problem.

Memory[0] = A
Memory[1] = B
Memory[2] = C
Memory[3] = D

mov Memory[0] P // P = A
mov Memory[1] Q // Q = B
mov Memory[2] R // R = C
mov Memory[3] S // S = D

cmp S P // compare D vs A
mov P T // T = A
cmovl S P // P = min(A, D)
cmovl T S // max(A, D)

cmp R P // compare C vs min(A, D)
mov P T // T = min(A, D) This instruction got eliminated
cmovg R P // P = max(C, min(A, D))
cmovl R T // T = min(A, C, D)

cmp Q T // compare B vs min(A, C, D)
mov T U // U = min(A, C, D)
cmovl Q U // U = min(A, B, C, D)
cmovl T Q // Q = max(B, min(A, C, D))

mov U Memory[0] // min(A, B, C, D)
mov Q Memory[1] // max(B, min(A, C, D))
mov P Memory[2] // max(C, min(A, D))
mov S Memory[3] // max(A, D)

As you can see, the algorithm discovered by AlphaDev is almost identical to the benchmark algorithm. However, AlphaDev eliminated one extra mov instruction. The question is whether the algorithm is still correct without that mov operation. Of course, DeepMind verified its correctness as part of their experiment; however, we need to convince ourselves.

The removed instruction is mov P T, which was setting the value min(A, D) as the value of the register T. Without this mov instruction, T remains with its original value, which is A.

Before the removed move operation, we are comparing C against min(A, D). If C < min(A, D), then the algorithm writes C into T; otherwise, T continues to store A. If we can show that the value in register T at this point is the same as the expression min(A, C, D), then the rest of the algorithm should also be correct because it is identical to the benchmark algorithm.

As we already know that D >= min(A, C), we can rewrite min(A, C, D) as min(A, C). So we just need to show that the value in register T is min(A, C).

Let’s first consider the case that C < min(A, D) and try to show that min(A, C) = C in this case.

min(A, D) has two possible values. If min(A, D) = A, then we have C < A, therefore min(A, C) = C.
However, if min(A, D) = D, then we have C < D < A, which again means C < A, or min(A, C) = C.

This shows that in the case C < min(A, D) we have the right value in register T. Next, let’s take the case that C > min(A, D). In this case, we need to show that min(A, C) = A, which is the value held in register T in this scenario.

Let’s say min(A, D) = A, then C > A, or min(A, C) = A.
On the other hand, if min(A, D) = D, then we have C > D. We also know that D >= min(A, C). Since C > D, min(A, C) cannot be C because it would contradict the inequality C > D. Hence, in this case also, min(A, C) = A which is the value stored in register T.

So in both cases, the register T ends up with the value min(A, C). As the rest of the algorithm after this step is identical to the benchmark, we can conclude that this implementation also produces correctly sorted output.

The eliminated mov instruction in the sort 4 algorithm has been termed as the AlphaDev Copy move.

Significance of AlphaDev's Optimization Discoveries

These optimizations might appear trivial and obvious, but it is important to note that the AlphaDev algorithm did not start with the benchmark algorithm and simply remove the mov instruction to arrive at the optimized implementation. AlphaDev began from scratch and incrementally built up the most optimized implementation by exploring the space of all possible implementations. The fact that it reached the same solution as the human benchmark and then surpassed it is the main highlight here. This means that the AlphaDev agent is capable of discovering similar optimizations in several other domains, as shown in the paper.

We should also note that while the optimization found by AlphaDev in the case of sort 3 seems very obvious, and many people would have been able to arrive at it themselves, the optimization for sort 4, although similar, was harder to verify by hand, and therefore fewer people could arrive at it. We can speculate that as we move towards higher complexity problems, the AI will be able to find more ingenious optimizations, which will be even more challenging for humans to recognize.

AlphaDev's Performance in Non-sorting Domains

In the paper, DeepMind primarily focused on showcasing the performance of AlphaDev on sorting problems. However, they also used it in other domains and observed that AlphaDev was able to find optimizations in diverse problem areas. For example, they have already used AlphaDev to discover a (non-cryptographic) hashing algorithm that was 30% faster.

Similarly, DeepMind employed AlphaDev to find a faster deserialization algorithm for variable-width integers in Google’s protobuf format. AlphaDev devised an efficient algorithm that was both shorter and up to 3 times faster than the human benchmark.

Lastly, DeepMind tested AlphaDev in competitive coding. They selected a contest problem and used AlphaDev to solve it with a customized reward function. AlphaDev found an optimal solution, which was intriguingly longer than the benchmark program but had lower latency. The agent figured out an efficient way to replace multiplication operations with addition and subtraction instructions.

Final Thoughts

In this article, we closely examined the algorithms discovered by AlphaDev for small sorting algorithms and compared them against the human benchmark implementations. We have been studying sorting algorithms for several decades, and humans are exceptionally skilled at hand-optimizing small pieces of code, such as sort 3 or sort 5. One might think there would not be much scope for improvement for sort 3 and sort 5, yet AlphaDev still managed to find small wins in them. And as these fixed length sorting routines are executed trillions of times a day, even a single instruction improvement is significant performance gain.

Hindsight is 20-20, and we can claim that these optimizations are not very impressive, but we need to consider two things here.

First, AlphaDev started from scratch and ended up finding the most optimal program. This is significant because AlphaDev is not an optimizer, but more like a program synthesizer that tries to find the most optimal programs for a given problem. This means that AlphaDev is capable of finding optimized solutions in various other areas.
Second, using AlphaDev on simpler problems, such as sort 3 or sort 5, allows us to examine the types of optimizations being found by the model and compare them against benchmarks. This experiment sets the stage for more complicated ones, as we will have a much better understanding of the agent's capabilities and the kind of clever tricks it can come up with.

Thank you for reading so far. I would love to know your views on AlphaDev. Do you also think that it is a marketing hype and not real discovery, or does it look promising to you? Let me know in the comments.